Modeling wind power output random process across multiple geographical locations

Specific Domains Modelling & Simulations
, ,
1

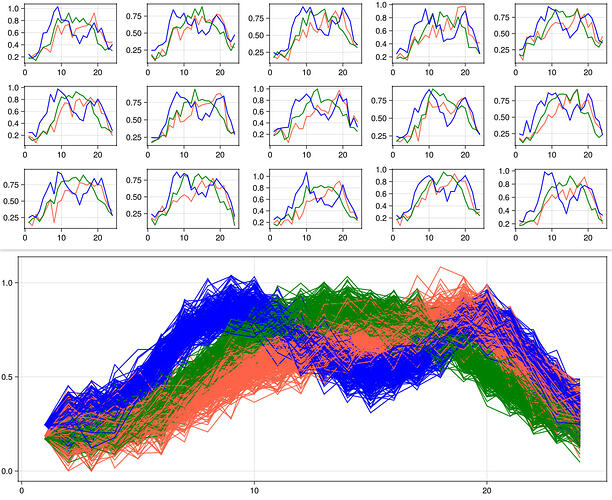
Hello,

I want to model a vector stochastic process (may be decided according to historical observations).

The length of the vector is N, which is the number of wind farms spreading in a power transmission network.
There are 24 hours in a day, denoted by T = 24.
I want to take account of temporal and spatial correlations.

A sample of the entire stochastic process should be a N-by-T matrix of wind power. Maybe the wind power of farm n at time t can be normalized to be in the interval [0, 1].

My minimum requirement about the uncertainty model is:

  • I need the conditional distribution of column t+1 given the realization of column t (in the matrix above). (Yes, (I assume) it has Markov property)

My question is:

  • Are there any advisable methods to build such an model realistically? (e.g. do I have to “transform” the numerics somehow (e.g. logistic function, z-score…)?)

Some additional notes:
My knowledge on statistics/regression/time series forecast is limited. And my knowledge on (engineering) wind power modeling is also zero.
I know there is a AR(1) model:

p_t = \mu + \Phi p_{t-1} + \epsilon_t

where \mu is a vector and \Phi is a matrix, both are weights to be decided on. And \epsilon_t is a stagewise independent error process (with multivariate normal distributions).

Since the \mu and \Phi do not depend on t, I naturally have a question here:

  • Can I build 23 separate (vector) linear regression models? (the first one models the transition from t=1 to t=2, the second one models the transition from t=2 to t = 3…) Suppose I have enough historical data. So I can decide the weights separately for each transition with the respective data. Will this be feasible? What’s the difference compared with a naive AR(1) model?

And finally I want to ask:

  • Are there any related mature julia packages in this regard?
2 Likes
2

It’s nice to see that more wind power researchers are using Julia!

Small remark: If you use LaTeX, enclose your formulas in $ signs.
This works nicely: \alpha \neq \beta

3

Spoiler alert: NaCl needed

  1. Normalization shouldn’t be required because you have a common dependent output variable, kWh.
  2. Temporal autocorrelation is to be expected because wind doesn’t suddenly increase and decrease frequently.
  3. Depending on how far about the wind farms are, spatial autocorrelation is also to be expected because they experience the same or similar wind velocities which may dominate differences in technologies among the farms. I haven’t found Ripley’s k in Julia, but rolling your own isn’t difficult.
  4. y = f(x), so wind is y? Then you need time series linear regression, not ARIMA.
  5. A good introductory text is Forecasting: Principles and Practice (3rd ed), although it’s R-based.
  6. My impression is that the Julia time series ecosystem is no so well developed as R’s. You may want to consider doing your data prep in Julia and time series in R.
  7. High-frequency time series modeling (hourly) generally produces better results using only the most recent data.
  8. Seasonality in wind patterns needs to be accommodated and may indicate separate models. STL decomposition should be looked at, and a Fourier transformation of data, also.
2 Likes