KernelAbstractions on CPU. Why so slow?

General Usage Performance
1

In the following code, launched with a single thread, KernelAbstractions’ function is almost twice slower than a simple broadcasting. Any ideas why?

using BenchmarkTools
using KernelAbstractions

@kernel function mulcab_kernel(C, A, B)
    i, j = @index(Global, NTuple)
    C[i,j] = A[i,j] * B[i,j]
end

function mulcab!(C, A, B)
    backend = get_backend(C)
    ndrange = size(C)
    mulcab_kernel(backend)(C, A, B; ndrange)
    return nothing
end

N = 2048
A = 2 * ones(N, N)
B = 3 * ones(N, N)
C = zeros(N, N)

@btime @. $C = $A * $B   # 4.038 ms (0 allocations: 0 bytes)

@btime mulcab!($C, $A, $B)   # 9.775 ms (10 allocations: 288 bytes)
2

Sadly the answer is not really interesting. You are simply lacking the @inbounds broadcast implicitly adds.

On my system:

julia> @btime @. $C = $A * $B 
  3.774 ms (0 allocations: 0 bytes)

julia> @btime mulcab!($C, $A, $B) 
  7.905 ms (9 allocations: 272 bytes)

After changing:

julia> @kernel function mulcab_kernel(C, A, B)
           i, j = @index(Global, NTuple)
           @inbounds C[i,j] = A[i,j] * B[i,j]
       end

julia> @btime mulcab!($C, $A, $B)   # 9.775 ms (10 allocations: 288 bytes)
  4.017 ms (9 allocations: 272 bytes)
2 Likes
3

Well, this is kind of unxpected for me. For example, the speed of the explicit loop function,

function mulcab_loop(C, A, B)
    N1, N2 = size(C)
    for j=1:N2, i=1:N1
        C[i,j] = A[i,j] * B[i,j]
    end
    return nothing
end

is the same as for the broadcasting, and the @inbounds macro has no effect on both of them. Does it mean that the compiler is smart enough to put @inbounds implicitly behind the scene?

4

Yes there is an LLVM optimization pass called InductiveRangeCheckElimination that can do boubds-checks elimination. The loop structure that KA uses under the hood is a bit more complicated so it might be that IRCE fails.

5

Great! Thank you. Very interesting to know.

If you allow, one more question. The problem above is an embarrassingly parallel one. Why the scaling with threads is so minor (see the plots below)?
N=2048 N=4096

6

Yes, but it also has a very low arithmetic intensity: for each multiplication operation, 3 memory accesses are needed (2 reads & 1 write). So I’d say the performances of this code are memory-bound: adding more CPUs won’t help as they have to wait for the data to be available.

The performance of this kernel is also likely to depend a lot on the size of your problem: if it is small enough to fit into the cache, memory accesses will be faster than for a large problem where data ultimately has to be fetched from RAM.

2 Likes
7

This may also be false sharing, along with high memory IO.

8

Thank you @ffevotte and @jmair.
Indeed, if I make the kernel more computationally intensive,

@kernel function mulcab_kernel(C, A, B)
    i, j = @index(Global, NTuple)
    @inbounds C[i,j] = exp(A[i,j]) * sin(B[i,j])
end

I start to see the expected behavior:
t_vs_nthreads

9

Another interesting observation. Using the following code:

using BenchmarkTools
using KernelAbstractions

func1(a, b) = a * b
func2(a, b) = exp(a) * sin(b)

function mulcab!(C, A, B)
    N1, N2 = size(C)
    for j=1:N2, i=1:N1
        C[i,j] = func2(A[i,j], B[i,j])
    end
    return nothing
end

@kernel function mulcab_kernel(C, A, B)
    i, j = @index(Global, NTuple)
    @inbounds C[i,j] = func2(A[i,j], B[i,j])
end
function mulcab_ka!(C, A, B)
    backend = get_backend(C)
    ndrange = size(C)
    mulcab_kernel(backend)(C, A, B; ndrange)
    return nothing
end

N = 2048   # 2 - 8192
A = 2 * ones(N, N)
B = 3 * ones(N, N)
C = zeros(N, N)

@btime mulcab!($C, $A, $B)

@btime mulcab_ka!($C, $A, $B)

I measured the computation times of simple loop and the corresponding KA kernel versus the size of the input array. I considered two cases: 1) low cost (func1(a, b) = a * b) and high cost (func2(a, b) = exp(a) * sin(b)) kernel function. The figures below show the resulting run time vs log2(N).

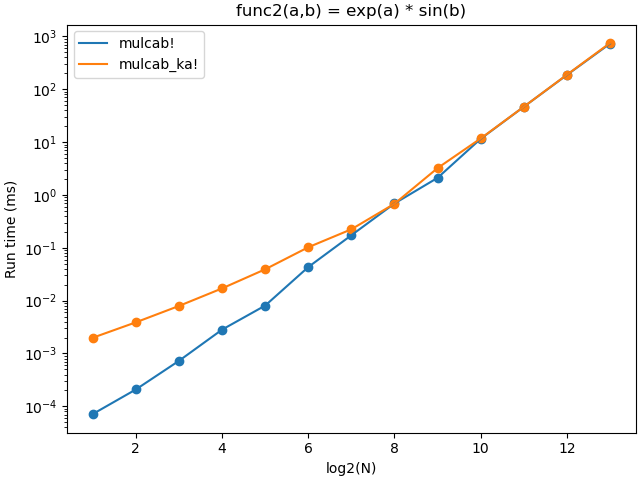
func1 func2

The figures show that KA introduce quite high overhead. For simple (memory bound) kernel, the overhead time becomes negligible starting from array sizes 1024x1024, while for more costly kernel, the corresponding array size is 128x128.

I guess, the conclusions can be the following. At present time KA introduce unpleasantly high overhead. Therefore, the recommendation is to combine small kernels into one big with high computational costs.