Improving GPU performance for symbolic regression

[MilesCranmer]

I’m trying to improve the GPU performance for evaluation of an expression represented as a tree in DynamicExpressions.jl. The way it works is that an expression is created at runtime – here’s a movie of how this is used in the context of SymbolicRegression.jl:

The bottleneck has always been in the evaluation of these expressions, and therefore that part has gone through many development cycles to get better perf.

To try to speed things up further I’m planning to allow the user to pass a CuArray for the dataset, so that the evaluation of these trees is faster.

Right now I have a recursive evaluation scheme that does a depth-first walk through the tree, building CUDA arrays at the leafs, and computing the operation at each node. This is my current code as drafted in this PR:

[removed; see below]

It uses an internal tree_mapreduce method which as the name suggests is a generalization of a regular mapreduce to a tree-like structure, so you can have different a “map” for leaf nodes or branch nodes, and aggregate on (parents, children...)

With this, I am seeing the following performance:

[removed; see below]

So it is sitting at about a 5.5x speedup. However, this 10,000 array size is actually larger than typical – you might only evaluate over a small batch of ~100 elements at a time. At that size, the CPU is ~microseconds while the GPU is stil at about 1.5ms.

Therefore I am wondering what my options are here to improve this. Is there something in the CUDA array operations I’m not doing correctly, which is perhaps causing the CUDA threads to sync before the next operation? Or is this fundamentally a limitation with this approach? It doesn’t seem possible to make a single CUDA kernel for this entire scheme, unfortunately.

Edit: see latest version here. It’s all done in a single CUDA kernel.

[Raf]

GPUs are almost never worth using for small arrays because kernel launch time will dwarf the operations, and 100 operations can only use a small fraction of your individually quite slow GPU cores anyway. Your few but super fast CPU cores will always eat problems like that for breakfast.

Try CUDA.@profile on your function for a breakdown of the timings.

There ares some things you can do. I’ve recently rewritten a bunch of my simulation code to handle this problem - I need replicates of every run (its stochastic) so I can stack 100 replicates of the array on another dimension to make it large enough to be worth launching a GPU kernel for.

But generally you need to have some single thing you need to do quite a few thousand times for it to be worth using a GPU.

[MilesCranmer]

Thanks. I was hoping there could be some way for it to lazily dispatch the calls to the GPU or something, since it does technically end up being 300x evaluations of the same array shape (just with this complex dependency structure which gets configured on the CPU) – and closer to the leafs of the tree, you can actually have many operations being executed at once, since they don’t depend on eachother. But maybe I’m being overly optimistic about what can be done automatically here.

I can also pre-compute the entire allocation needed (= 150 x 100 elements for batch size of 100 and 150 leaf nodes) in advance; would that maybe help at all? It would still have this graph of calculation dependencies but it at least wouldn’t need to create allocations repeatedly.

[MilesCranmer]

I wonder if it’s also possible to do this entire thing in a single CUDA kernel on a preallocated storage array? The tricky thing is you would need to have a particular dependency structure for the threads so that the leaf nodes execute first, the (depth-1) nodes second, and so on. But you could totally generate all of that information on the CPU before making the kernel call, and pass it as an array to the GPU.

julia> using DynamicExpressions

julia> operators = OperatorEnum(binary_operators=(+, -, *, /), unary_operators=(cos, sin));

julia> x1, x2, x3 = [Node{Float64}(feature=i) for i in 1:3];

julia> tree = cos(x1) * x2 - 0.9 / x3; for _=1:2; tree=cos(tree) - 0.9*tree; end; tree
cos(cos((cos(x1) * x2) - (0.9 / x3)) - (0.9 * ((cos(x1) * x2) - (0.9 / x3)))) - (0.9 * (cos((cos(x1) * x2) - (0.9 / x3)) - (0.9 * ((cos(x1) * x2) - (0.9 / x3)))))

julia> local_depth = count_depth.(collect(nodes));
5-element Vector{Int64}:
 8
 7
 6
 5
 4

This local_depth would be the depth at each node position, and basically tells you the execution order so that all dependent parts of the computation are executed beforehand. i.e., leaf nodes (like constants or features) would have a depth of 1, so they are executed first.

[MilesCranmer]

Edit: out-of-date; see next post!

[MilesCranmer]

Quick update – got it working with a single CUDA kernel! Here’s the code.

(click to expand)

module DynamicExpressionsCUDAExt
#! format: off

using CUDA
using DynamicExpressions: OperatorEnum, AbstractExpressionNode
using DynamicExpressions.EvaluateEquationModule: get_nbin, get_nuna
using DynamicExpressions.AsArrayModule: as_array

import DynamicExpressions.EvaluateEquationModule: eval_tree_array

function eval_tree_array(
    tree::AbstractExpressionNode{T}, gcX::CuArray{T,2}, operators::OperatorEnum; _...
) where {T<:Number}
    (outs, is_good) = eval_tree_array((tree,), gcX, operators)
    return (only(outs), only(is_good))
end

function eval_tree_array(
    trees::NTuple{M,N}, gcX::CuArray{T,2}, operators::OperatorEnum; _...
) where {T<:Number,N<:AbstractExpressionNode{T},M}
    (; val, execution_order, roots, buffer) = as_array(Int32, trees...)
    num_launches = maximum(execution_order)
    num_elem = size(gcX, 2)
    num_nodes = size(buffer, 2)

    ## Floating point arrays:
    gworkspace = CuArray{T}(undef, num_elem, num_nodes)
    gval = CuArray(val)

    ## Index arrays (much faster to have `@view` here)
    gbuffer = CuArray(buffer)
    gdegree = @view gbuffer[1, :]
    gfeature = @view gbuffer[2, :]
    gop = @view gbuffer[3, :]
    gexecution_order = @view gbuffer[4, :]
    gidx_self = @view gbuffer[5, :]
    gidx_l = @view gbuffer[6, :]
    gidx_r = @view gbuffer[7, :]
    gconstant = @view gbuffer[8, :]

    num_threads = 256
    num_blocks = nextpow(2, ceil(Int, num_elem * num_nodes / num_threads))

    _launch_gpu_kernel!(
        num_threads, num_blocks, num_launches, gworkspace,
        # Thread info:
        num_elem, num_nodes, gexecution_order,
        # Input data and tree
        operators, gcX, gidx_self, gidx_l, gidx_r,
        gdegree, gconstant, gval, gfeature, gop,
    )

    out = ntuple(
        i -> @view(gworkspace[:, roots[i]]),
        Val(M)
    )
    is_good = ntuple(
        i -> true,  # Up to user to find NaNs
        Val(M)
    )

    return (out, is_good)
end

function _launch_gpu_kernel!(
    num_threads, num_blocks, num_launches::Integer, buffer::AbstractArray{T,2},
    # Thread info:
    num_elem::Integer, num_nodes::Integer, execution_order::AbstractArray{I},
    # Input data and tree
    operators::OperatorEnum, cX::AbstractArray{T,2}, idx_self::AbstractArray, idx_l::AbstractArray, idx_r::AbstractArray,
    degree::AbstractArray, constant::AbstractArray, val::AbstractArray{T,1}, feature::AbstractArray, op::AbstractArray,
) where {I,T}
    nuna = get_nuna(typeof(operators))
    nbin = get_nbin(typeof(operators))
    (nuna > 10 || nbin > 10) && error("Too many operators. Kernels are only compiled up to 10.")
    gpu_kernel! = create_gpu_kernel(operators, Val(nuna), Val(nbin))
    for launch in one(I):I(num_launches)
        @cuda threads=num_threads blocks=num_blocks gpu_kernel!(
            buffer,
            launch, num_elem, num_nodes, execution_order,
            cX, idx_self, idx_l, idx_r,
            degree, constant, val, feature, op
        )
    end
    return nothing
end

# Need to pre-compute the GPU kernels with an `@eval` for each number of operators
#   1. We need to use an `@nif` over operators, as GPU kernels
#      can't index into arrays of operators.
#   2. `@nif` is evaluated at parse time and needs to know the number of
#      ifs to generate at that time, so we can't simply use specialization.
#   3. We can't use `@generated` because we can't create closures in those.
for nuna in 0:10, nbin in 0:10
    @eval function create_gpu_kernel(operators::OperatorEnum, ::Val{$nuna}, ::Val{$nbin})
        function (
            # Storage:
            buffer,
            # Thread info:
            launch::Integer, num_elem::Integer, num_nodes::Integer, execution_order::AbstractArray,
            # Input data and tree
            cX::AbstractArray, idx_self::AbstractArray, idx_l::AbstractArray, idx_r::AbstractArray,
            degree::AbstractArray, constant::AbstractArray, val::AbstractArray, feature::AbstractArray, op::AbstractArray,
        )
            i = (blockIdx().x - 1) * blockDim().x + threadIdx().x
            if i > num_elem * num_nodes
                return nothing
            end

            node = (i - 1) % num_nodes + 1
            elem = (i - node) ÷ num_nodes + 1

            if execution_order[node] != launch
                return nothing
            end

            cur_degree = degree[node]
            cur_idx = idx_self[node]
            if cur_degree == 0
                if constant[node] == 1
                    cur_val = val[node]
                    buffer[elem, cur_idx] = cur_val
                else
                    cur_feature = feature[node]
                    buffer[elem, cur_idx] = cX[cur_feature, elem]
                end
            else
                if cur_degree == 1
                    cur_op = op[node]
                    l_idx = idx_l[node]
                    Base.Cartesian.@nif(
                        $nuna,
                        i -> i == cur_op,
                        i -> let op = operators.unaops[i]
                            buffer[elem, cur_idx] = op(buffer[elem, l_idx])
                        end
                    )
                else
                    cur_op = op[node]
                    l_idx = idx_l[node]
                    r_idx = idx_r[node]
                    Base.Cartesian.@nif(
                        $nbin,
                        i -> i == cur_op,
                        i -> let op = operators.binops[i]
                            buffer[elem, cur_idx] = op(buffer[elem, l_idx], buffer[elem, r_idx])
                        end
                    )
                end
            end
            return nothing
        end
    end
end

#! format: on
end

The key function is _launch_gpu_kernel which actually launches the kernels. Basically, each launch, it goes one up the tree to the next node that can be computed, and spawns all the threads to all (array elements) x (available nodes).

In gif form, the CUDA launches are like this:

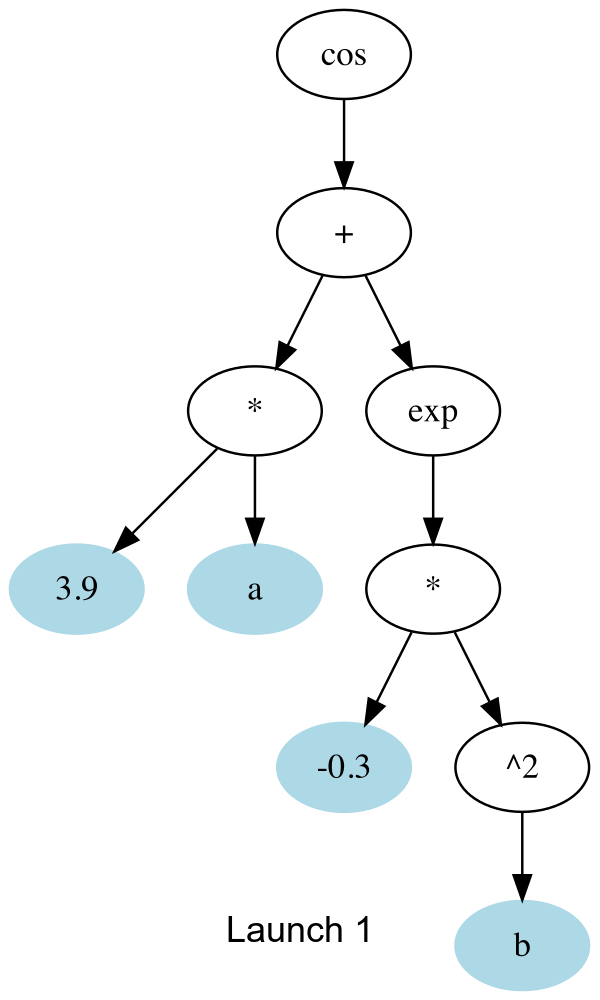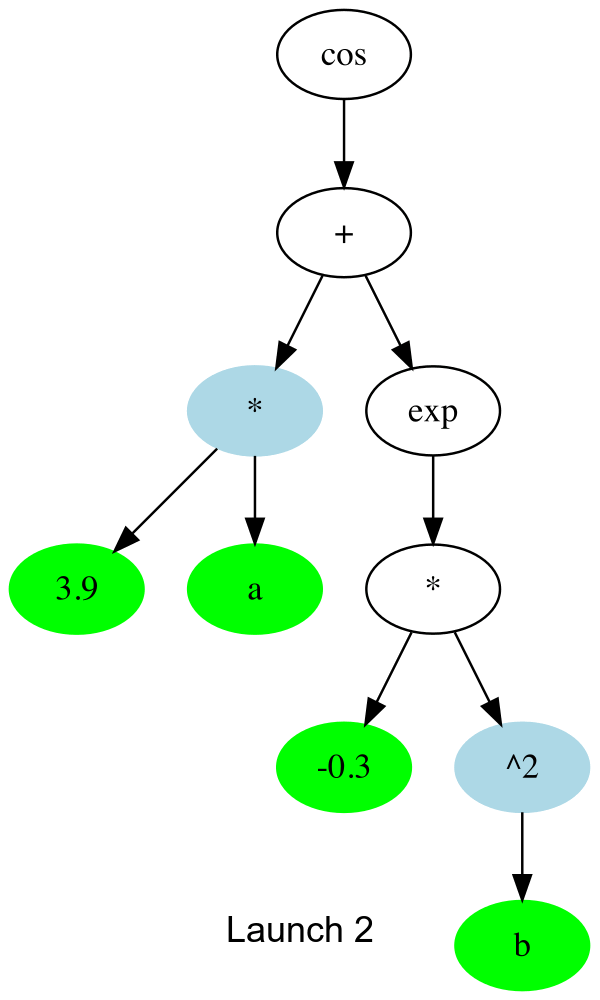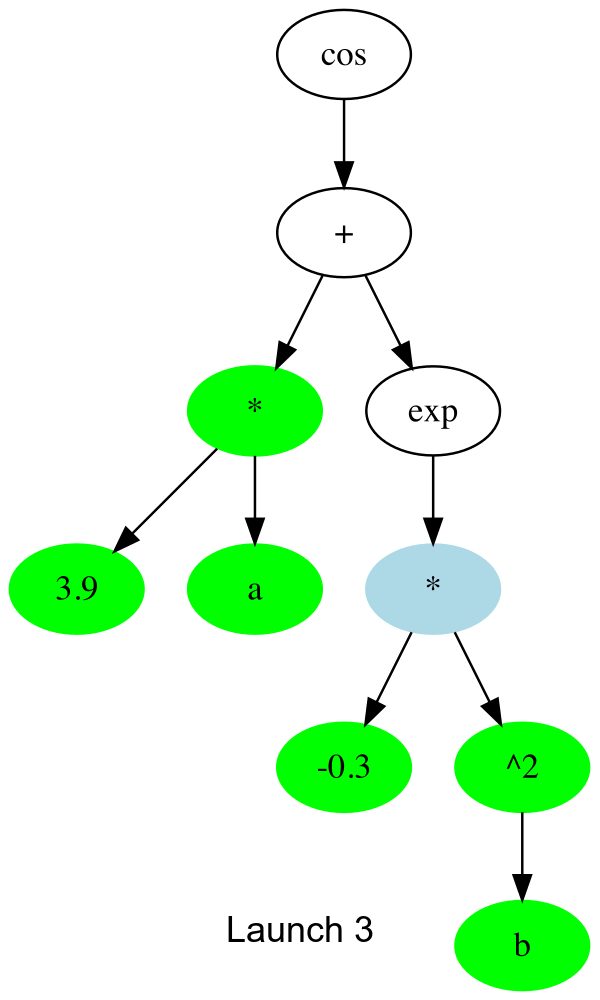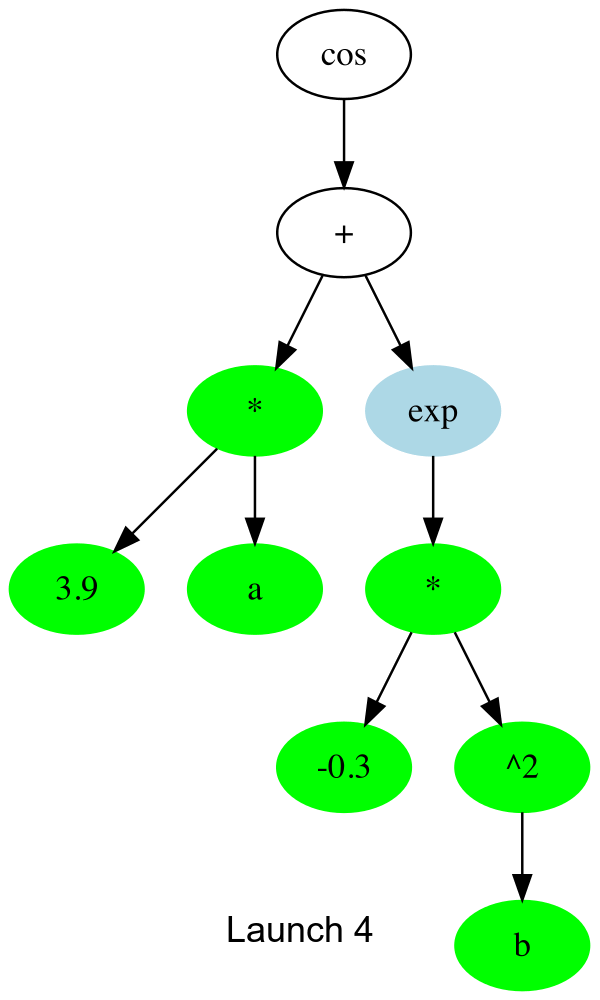
And the threads which don’t compute anything simply quit early. This is about 30% faster than the initial naive version I tried. I’m assuming there’s remaining slowness due to me misusing some part of CUDA.jl, so any other tips much appreciated

Also I want to note that this new attempt allows batching over expressions! So you can do, e.g.,

julia> eval_tree_array((tree1, tree2, tree3), X, operators)

and it will put them in one big array and work on them at the same time. So maybe this is a way to get your suggestion working @Raf – I need to find a way to batch evaluate over expressions.

Finally, here’s the profiling results:

julia> CUDA.@profile eval_tree_array(tree, X, operators)[1]
Profiler ran for 638.25 µs, capturing 376 events.

Host-side activity: calling CUDA APIs took 377.89 µs (59.21% of the trace)
┌──────────┬────────────┬───────┬───────────────────────────────────────┬─────────────────────────┐
│ Time (%) │ Total time │ Calls │ Time distribution                     │ Name                    │
├──────────┼────────────┼───────┼───────────────────────────────────────┼─────────────────────────┤
│   21.93% │  139.95 µs │    27 │   5.18 µs ± 15.46  (  1.43 ‥ 82.49)   │ cuMemAllocFromPoolAsync │
│   19.24% │  122.79 µs │    31 │   3.96 µs ± 3.28   (  2.62 ‥ 20.98)   │ cuLaunchKernel          │
│    5.53% │   35.29 µs │     9 │   3.92 µs ± 4.71   (  2.15 ‥ 16.45)   │ cuMemcpyHtoDAsync       │
│    2.69% │   17.17 µs │     1 │                                       │ cuMemcpyDtoHAsync       │
│    1.57% │   10.01 µs │    11 │ 910.33 ns ± 381.74 (476.84 ‥ 1668.93) │ cuStreamSynchronize     │
└──────────┴────────────┴───────┴───────────────────────────────────────┴─────────────────────────┘

Device-side activity: GPU was busy for 188.59 µs (29.55% of the trace)
┌──────────┬────────────┬───────┬─────────────────────────────────────┬──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ Time (%) │ Total time │ Calls │ Time distribution                   │ Name                                                                                                                                                                                        ⋯
├──────────┼────────────┼───────┼─────────────────────────────────────┼──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│   21.52% │  137.33 µs │    14 │   9.81 µs ± 1.72   (  6.91 ‥ 12.87) │ _Z3_5913CuDeviceArrayI7Float32Li2ELi1EE5Int64S1_S_I4BoolLi1ELi1EES_IS0_Li2ELi1EES_I5Int32Li1ELi1EES_IS3_Li1ELi1EES_IS3_Li1ELi1EES_I5UInt8Li1ELi1EES_IS2_Li1ELi1EES_IS0_Li1ELi1EES_I6UInt16L ⋯
│    4.41% │   28.13 µs │    14 │   2.01 µs ± 0.12   (  1.91 ‥ 2.15)  │ _Z16broadcast_kernel15CuKernelContext13CuDeviceArrayI4BoolLi1ELi1EE11BroadcastedI12CuArrayStyleILi1EE5TupleI5OneToI5Int64EE2__S4_I8ExtrudedIS0_I5Int32Li1ELi1EES4_IS1_ES4_IS6_EES9_EES6_    ⋯
│    1.91% │   12.16 µs │     9 │   1.35 µs ± 0.12   (  1.19 ‥ 1.43)  │ [copy pageable to device memory]                                                                                                                                                            ⋯
│    0.67% │    4.29 µs │     1 │                                     │ _Z22partial_mapreduce_grid8identity7add_sum7Float3216CartesianIndicesILi1E5TupleI5OneToI5Int64EEES2_ILi1ES3_IS4_IS5_EEE3ValILitrueEE13CuDeviceArrayIS1_Li2ELi1EE11BroadcastedI12CuArrayStyl ⋯
│    0.41% │    2.62 µs │     1 │                                     │ _Z16broadcast_kernel15CuKernelContext13CuDeviceArrayI7Float32Li1ELi1EE11BroadcastedI12CuArrayStyleILi1EE5TupleI5OneToI5Int64EE1_S4_I8ExtrudedIS0_IS1_Li1ELi1EES4_I4BoolES4_IS6_EES1_EES6_   ⋯
│    0.37% │    2.38 µs │     1 │                                     │ _Z15getindex_kernel15CuKernelContext13CuDeviceArrayI7Float32Li1ELi1EES0_IS1_Li2ELi1EE5TupleI5Int64S3_E5SliceI5OneToIS3_EES3_                                                                ⋯
│    0.26% │    1.67 µs │     1 │                                     │ [copy device to pageable memory]                                                                                                                                                            ⋯
└──────────┴────────────┴───────┴─────────────────────────────────────┴──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
                                                                                                                                                                                                                                                     1 column omitted

---

Edit: Improved some of the redundant allocations. Now I’m seeing the GPU have a 3x improvement in perf on even 1,000 element arrays.

[Zentrik]

I haven’t looked through your code thoroughly so some general tips I would have are use 32 bit integers and floats if possible, don’t use recursion but instead a for/while loop and inline aggressively. Check out Performance Tips · CUDA.jl

EDIT: you don’t seem to be using recursion in the kernel so ignore that. One other thing would be using a grid stride loop so that you can use the optimal thread/ block sizes according to the occupancy calculator. I’m not sure that would be a big benefit though.

[MilesCranmer]

The CPU evaluation is recursion based (I tried a stack-based one a while ago but it didn’t make any difference and had a much greater complexity). But the new GPU one does everything in parallel for expression tree nodes which are independent from one another. Let me update the first post because that’s an older version.

There’s no recursion and the only for loop right now is in the _launch_gpu_kernel! part is to avoid data races (see gif above). So it looks like this:

function _launch_gpu_kernel!(
    num_threads, num_blocks, num_launches::Integer, buffer::AbstractArray{T,2},
    # Thread info:
    num_elem::Integer, num_nodes::Integer, execution_order::AbstractArray{I},
    # Input data and tree
    operators::OperatorEnum, cX::AbstractArray{T,2}, idx_self::AbstractArray, idx_l::AbstractArray, idx_r::AbstractArray,
    degree::AbstractArray, constant::AbstractArray, val::AbstractArray{T,1}, feature::AbstractArray, op::AbstractArray,
) where {I,T}
    nuna = get_nuna(typeof(operators))
    nbin = get_nbin(typeof(operators))
    (nuna > 10 || nbin > 10) && error("Too many operators. Kernels are only compiled up to 10.")
    gpu_kernel! = create_gpu_kernel(operators, Val(nuna), Val(nbin))
    for launch in one(I):I(num_launches)
        @cuda threads=num_threads blocks=num_blocks gpu_kernel!(
            buffer,
            launch, num_elem, num_nodes, execution_order,
            cX, idx_self, idx_l, idx_r,
            degree, constant, val, feature, op
        )
    end
    return nothing
end

Every GPU thread checks the launch integer here to see if it is its turn to execute; otherwise it exits. But if there’s a better way to force the threads to run in a particular order (without needing to dispatch again and again) I’d love to hear it.

[MilesCranmer]

I also made some improvements to the memory allocation. It seems like each new call to CuArray is the bottleneck right now, so the new version (updated the code) uses views of a large array of integers (even for Bool). This helps a lot.

Surprisingly those parts are still the bottleneck though (more typical array size used for this) –

I’m wondering if there’s any way I can just have a single CuArray call at the top and use @view and interpret the bits as Float32/Int32 as needed. Is that possible here?

[MilesCranmer]

Alright so that big red bar in that flame graph turned out to be this call in CUDA.jl in execution.jl:

function (kernel::HostKernel)(args...; threads::CuDim=1, blocks::CuDim=1, kwargs...)
    call(kernel, map(cudaconvert, args)...; threads, blocks, kwargs...)
end

If I simply apply this change to it:

-  function (kernel::HostKernel)(args...; threads::CuDim=1, blocks::CuDim=1, kwargs...)
+  function (kernel::HostKernel)(args::Vararg{Any,M}; threads::CuDim=1, blocks::CuDim=1, kwargs...) where {M}

this makes it specialize and gets another 20% improvement!

This is because Vararg doesn’t automatically specialize Performance Tips · The Julia Language – so that map(cudaconvert, args)... call causes a bit of damage.

@maleadt are you okay if we upstream this change?

[Zentrik]

Does the VSCode profiler (I assume that’s what you’re using) profile GPU code? I don’t think it does.

[maleadt]

@MilesCranmer

@maleadt are you okay if we upstream this change?

Yeah, I think that would be fine!

[MilesCranmer]

Cool. Done! Fix dynamic dispatch issue by MilesCranmer · Pull Request #2235 · JuliaGPU/CUDA.jl · GitHub