It’s worth noting that there are two different perspectives that have sometimes incompatible behaviors:
Image as 2D Histogram
If I understand correctly you’re looking at the image as a 2D histogram, so each pixel is a box around a set of events, and resizing those boxes shouldn’t change the total number of events. Making the boxes bigger by an integer factor (e.g. from 8x8 to 4x4) seems well-defined, because you can sum collections of adjacent boxes. Resizing in the other direction seems tough because you don’t know how many of the original events were in each region of the larger boxes.
Image as Samples
In a DSP context the pixels aren’t boxes, they’re points representing samples of an underlying continuous 2D image. The continuous signal is assumed to be bandlimited (it’s “smooth” such that it doesn’t wiggle faster than the samples can represent).
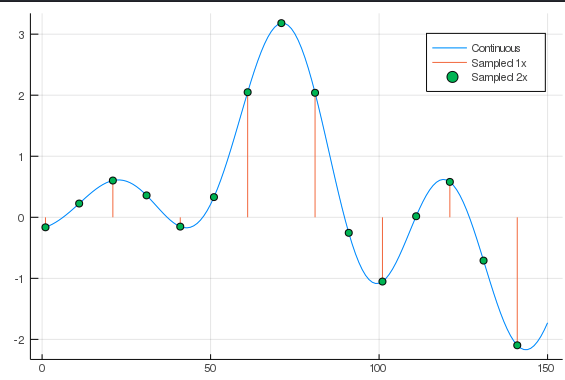
Resampling in this context is is a matter of sampling the continuous surface at different points. So if you’re upsampling by 2 then you’re sampling the continuous function between the existing samples, but they are not generally a simple average of the samples on either side. Here’s the picture to have in mind (in 1D rather than 2D), where the orange lines show the original samples and the green dots are the new samples.
Downsampling is a little more complicated because the bandlimited requirement means the function needs to be smoother (because your samples are farther apart). That’s what an “anti-aliasing” filter does.
Rebinning the histogram
As you mention, downsampling by an integer factor is the easy case - you could just convolve your image with an ones(N, N) where N is your downsample factor:
using DSP
x = rand(32, 32)
x ./= sum(x) #normalize to 1
sum(x) # gives 1
w = ones(2,2)
y = conv(x,w)[2:2:32, 2:2:32] # do the sum and then pick out every other sample
sum(y) # gives 1
One way to upsample (by an integer factor) would just be to divide each bin into smaller ones and distribute the events evenly:
x = rand(16, 16)
x ./= sum(x) # normalize to 1
sum(x) # gives 1
y = zeros(32, 32)
# first copy into the larger array, leaving gaps for the new bins
y[1:2:32,1:2:32] .= x
# now we redistribute the events to fill the gaps
w = ones(2,2) ./ 4
y = conv(y, w)[1:32, 1:32]
sum(y) # gives 1
Different interpolation schemes basically amount to changing the window w. For instance, using a window of ones(3,3) / 9 will do linear interpolation, but creates a problem on the bottom and right edges of the image, because those pixels don’t have pixels on both sides to average.
The next step from integer resampling is rational resampling, where your factor is A//B. In this case you can upsample by A and downsample by B (though that’s not the most efficient way). Irrational resampling is trickier, I’d definitely use a package for that.