I have a performance critical call to set bounds on a number. This code works like magic, but I want to know why it doesn’t need to allocate
julia> @benchmark clamp(v[1],extrema((v[2],v[3],v[4]))...) setup=(v=rand(4))
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 8.571 ns (0.00% GC)
median time: 9.320 ns (0.00% GC)
mean time: 9.318 ns (0.00% GC)
maximum time: 27.229 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 999
So again, I love this solution. It is extremely readable. But I need to create a tuple for extrema which seems like it should require an allocation. For example, this is mathematically equivalent
julia> @benchmark median((v[1],v[1],v[2],v[3],v[4])) setup=(v=rand(4))
BenchmarkTools.Trial:
memory estimate: 128 bytes
allocs estimate: 1
--------------
minimum time: 94.199 ns (0.00% GC)
median time: 103.288 ns (0.00% GC)
mean time: 108.575 ns (1.64% GC)
maximum time: 1.196 μs (81.55% GC)
--------------
samples: 10000
evals/sample: 957
but requires an allocation and so is 10x slower. I tried median(SArray(v[1],v[1],v[2],v[3],v[4])) and median((v[1],v[2],median((v[1],v[3],v[4])))) but they all allocate.
Is this something special about extrema or something general about Julia I should understand? Or maybe @benchmarktools is lying to me?
extrema iterates over elements and keeps track of the min and max. So it does not allocate. See line 1711 of https://github.com/JuliaLang/julia/blob/master/base/multidimensional.jl
median needs to sort and therefore allocate a vector.
If you can pass v as a Vector, median! does not allocate:
julia> @benchmark median!(v) setup=(v=rand(4))
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 15.952 ns (0.00% GC)
median time: 16.424 ns (0.00% GC)
mean time: 17.729 ns (0.00% GC)
maximum time: 91.392 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 997
2 Likes
Thanks, that makes sense. Unfortunately, the bounds aren’t constant, so I would need to refill the whole array every call.
In this case it looks like a custom function wins the race!
@fastmath function median(a,b,c)
x = a-b
if x*(b-c) ≥ 0
return b
elseif x*(a-c) > 0
return c
else
return a
end
end
julia> @benchmark median(v[2],v[1],median(v[3],v[1],v[4])) setup=(v=rand(4))
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 2.399 ns (0.00% GC)
median time: 3.400 ns (0.00% GC)
mean time: 3.264 ns (0.00% GC)
maximum time: 26.301 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
Plus this code is especially fast if the value is within the bounds (which is usually the case).
julia> @benchmark median(v[1],m,median(v[2],m,v[3])) setup=(v=rand(3);m=mean(v))
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 2.399 ns (0.00% GC)
median time: 2.500 ns (0.00% GC)
mean time: 2.769 ns (0.00% GC)
maximum time: 75.501 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
2 Likes
I think you can make that function faster and more self-explanatory by replacing the multiplications by comparisons.
if a>b
b>=c && return b
a>c && return c
else
b<=c && return b
a<c && return c
end
return a
(Disclaimer: I’m on my phone, and I’m not entirely sure what your function is supposed to do so this might be a bit misspelled, but the idea holds)
1 Like
That’s the same speed on my system, but you’re right that it is more readable. Thanks!
If you rewrite it
function fun(a, b, c)
(a>b)*(b>=c) && return b
(a>b)*(a>c) && return c
return a
end
it only has to perform boolean mutliplications;
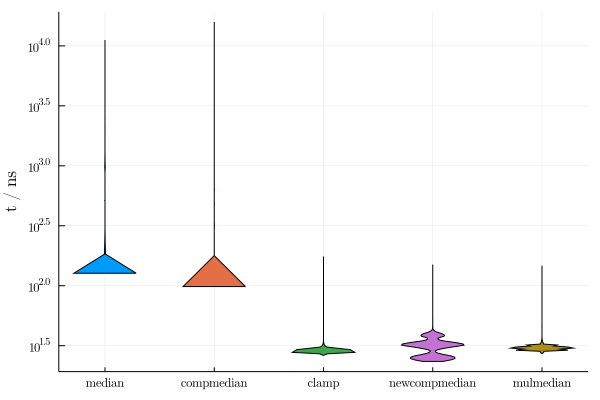
“newcompmedian” is the new one. I’m guessing the three modes there correspond to shortcutting after 1, 2 or 3 comparisons.
1 Like
Cool! Can you post the code for this? I would love to take a look.
Did it in the REPL (stupidly), but
using BenchmarkTools, StatsPlots, BenchmarkPlots # Requires this pull request: https://github.com/JuliaCI/BenchmarkTools.jl/pull/194/commits/230663872002eae1f9513590f68322636f2fa05d
default(fontfamily="Computer Modern")
function mulmedian(a, b, c)
x = a-b
if x*(b-c) >= 0
return b
elseif x*(a-c) > 0
return c
else
return a
end
end
function compmedian(a, b, c)
if a>b
b>=c && return b
a>c && return c
else
b<=c && return b
a<c && return c
end
return a
end
function newcompmedian(a, b, c)
xor((a>b), (b<=c)) && return b
xor((a>b), (a<c)) && return c
return a
end
clampfun(v) = clamp(v[1], extrema((v[2],v[3],v[4]))...)
medianfun(v) = median((v[1],v[1],v[2],v[3],v[4]))
mulmedianfun(v) = mulmedian(v[2], v[1], mulmedian(v[3], v[1], v[4]))
compmedianfun(v) = compmedian(v[2], v[1], compmedian(v[3], v[1], v[4]))
newcompmedianfun(v) = newcompmedian(v[2], v[1], newcompmedian(v[3], v[1], v[4]))
suite = BenchmarkGroup()
suite["clamp"] = @benchmarkable clampfun(v) setup=(v=rand(4))
suite["median"] = @benchmarkable medianfun(v) setup=(v=rand(4))
suite["mulmedian"] = @benchmarkable mulmedianfun(v) setup=(v=rand(4))
suite["compmedian"] = @benchmarkable compmedianfun(v) setup=(v=rand(4))
suite["newcompmedian"] = @benchmarkable newcompmedianfun(v) setup=(v=rand(4))
results = run(suite)
plot(results; yscale=:log10)
2 Likes
Of note here, though, (a>b)*(b >= c) is not equal to (a-b)*(b-c) >= 0
julia> a, b, c = 1, 2, 3
(1, 2, 3)
julia> (a > b) *(b >= c)
false
julia> (a - b)*(b - c) >=0
true
Yeah, you’re right. I meant xor. Which actually makes it a bit faster. Edited.
I do not quite understand, why xor is better
julia> xor((a>b), (b>=c))
false
I think proper formula is
julia> (a == b) | (b == c) | ((a > b)&(b>c)) | ((a < b)&(b < c))
true
but it is rather slow.
If (a-b)*(b-c) >= 0, then both parentheses are >=0, or they are both <=0. Depending on how sensitive the application is to the difference between <= and < (I still don’t quite understand what we are doing here, but it’s some kind of sorting/clamping thing so it shouldn’t matter), you can use xor((a>=b), (b<c)). Or some other combination of comparisons. Shouldn’t matter much for the timings.
We’re ensuring that a number is within the extrema of three other numbers. The clamp function version is certainly the most direct and since it doesn’t use any custom code, it could be used to unit test any of the other versions.
I’m happy to do so but (dumb question) how do I get your PR above? Do I need to git fetch https://github.com/JuliaCI/BenchmarkTools.jl/pull/194/commits/230663872002eae1f9513590f68322636f2fa05d
I’m not sure if there’s a native way to select a specific commit, but ]dev https://github.com/gustaphe/BenchmarkTools.jl/ should do the job for now because it’s on my master branch.
1 Like
Perhaps a bit of a tangent, but here’s an attempt at at a non-allocating median for tuples, by simply listing all the options. This will end up making the same comparison many times, and only works for short tuples, surely there is a better algorithm:
using Combinatorics, Statistics
function _medex(n)
out = quote end
for p in permutations(1:n)
z = zip(Iterators.repeated(:(<=)), [:(x[$i]) for i in p])
c = Expr(:comparison, Iterators.drop(Iterators.flatten(z),1)...)
v = isodd(n) ? :(x[$(p[1+n÷2])]) : :((x[$(p[n÷2])] + x[$(p[1+n÷2])])/2)
push!(out.args, :($c && return $v))
end
out
end
_medex(3) # to see what this generates
@generated unrollmedian(x::Tuple) = _medex(length(x.parameters))
unrollmedian(xs::Number...) = unrollmedian(xs)
for n in 2:6
x = Tuple(rand(Int8,n))
@show n
@btime median($(Ref(x))[])
@btime unrollmedian($(Ref(x))[]) # at n=7 I have to kill julia
end
using Random, Statistics, BenchmarkTools
Statistics.median(xs::Number...) = median(xs) # to match @gustaphe's functions
Random.seed!(1);
xs = Tuple(rand(Int8, 3)) # (64, 82, -103)
for f in [median, unrollmedian, fastmath_median, fun, mulmedian, compmedian, newcompmedian]
@show f f(xs...)
@btime $f($(Ref(xs))[]...)
end
This comparison prints the following, note that several functions above give the wrong answer, I think they assume that all numbers are positive. Not sure how meaningful these tiny times are:
f = Statistics.median
f(xs...) = -82.0
26.439 ns (1 allocation: 96 bytes)
f = unrollmedian
f(xs...) = -82
1.208 ns (0 allocations: 0 bytes)
f = fastmath_median
f(xs...) = 103
0.916 ns (0 allocations: 0 bytes)
f = fun
f(xs...) = -82
1.292 ns (0 allocations: 0 bytes)
f = mulmedian
f(xs...) = 103
0.916 ns (0 allocations: 0 bytes)
f = compmedian
f(xs...) = -82
1.166 ns (0 allocations: 0 bytes)
f = newcompmedian
f(xs...) = -82
1.333 ns (0 allocations: 0 bytes)
I can confirm that newcompmedian doesn’t work. If a<b<c then xor( a>b, b>=c ) = xor(false,false)=false which means it misses b as the median.
This one seems to work
function eqcompmedian(a, b, c)
(a>b) == (b>=c) && return b
(a>b) == (a>c) && return c
return a
end
I think this is exactly the same logical chain as mulmedian. When doing the timing, I get
julia> run(suite)
5-element BenchmarkTools.BenchmarkGroup:
tags: []
"median" => Trial(144.000 ns)
"compmedian" => Trial(43.000 ns)
"eqcompmedian" => Trial(45.000 ns)
"clamp" => Trial(63.000 ns) # this one seems quite variable??
"mulmedian" => Trial(47.000 ns)
So compmedian is the best by a hair.
Yeah, it would have to be opposite comparisons. (a>b) == (b>=c) <==> ~xor((a>b), (b<c)). Don’t know if there’s any performance implication.
That works! On my machine all of the double median version are essentially the same. Clamp is a little slower (actually, still pretty much the same) and the single vectorized median is much worse due to the allocation.
@mcabbot, in case it might interest, for larger lists of numbers, a median finding algorithm, seemingly faster than sort-based methods, is presented in a simple way here and the author points also to a more advanced reference on this topic by Andrei Alexandrescu.
1 Like
