3D isosurface plotting in Makie

[mreichMPI-BGC]

I am using the (semi-)documented contour function for 3D-isosurfaces, cf. volume | Makie, first example.

One cannot define vector of alphas (which would be nice because outer surfaces (shells) “should” be more transparent.

Thus I came up with the following code:

using Statistics, GLMakie, LinearAlgebra

_iscollection(x) = x isa Union{AbstractArray, Tuple, AbstractRange}
# Cycle collections; repeat scalars
_as_iter(x, n) = _iscollection(x) ? Iterators.take(Iterators.cycle(x), n) :
                                   Iterators.repeated(x, n)

function new_iso_contour3d!(
    vol::AbstractArray;
    xs = (1, size(vol, 1)), ys = (1,size(vol, 2)), zs = (1,size(vol, 3)),
    ax = current_axis(),
    levels = quantile(vol, [0.25, 0.50, 0.75]),
    colors = [:yellow, :orange, :red],
    alphas = [0.05, 0.1, 0.2],
)

    lvls = levels isa Number ? (levels, ) : collect(levels)
    L = length(lvls)
    cols = collect(_as_iter(colors, L))
    als  = collect(_as_iter(alphas, L))

    ivx, ivy, ivz = extrema(xs), extrema(ys), extrema(zs)

    for (lev, col, a) in zip(lvls, cols, als)
        contour!(ax, ivx, ivy, ivz, vol;
                 levels=[lev], colormap=cgrad([col, col]), alpha=a)
    end
    nothing
end

r = range(-1, 1, length=20)
vol = [norm([1.2x,y,z]) for x=r, y=r, z=r]
fig = Figure()
ax = LScene(fig[1, 1], scenekw=(show_axis=true,))
new_iso_contour3d!(vol[1:10,:,:]; xs=0.5r, ys=r, zs=r,
    levels=[0.1, 0.5, 0.8], colors=[:red, :orange, :yellow], alphas=[0.2, 0.1, 0.05])

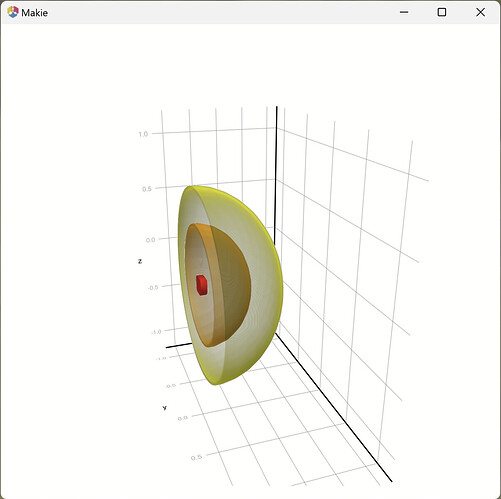
Now, my problem is that the isosurfaces are very thick:

I also tried volume(algorithm=:iso,…) and then a thin isorange, but with smaller alpha the surfaces are really grey. So it would be nice to have control over isorange also from the contour function (?).

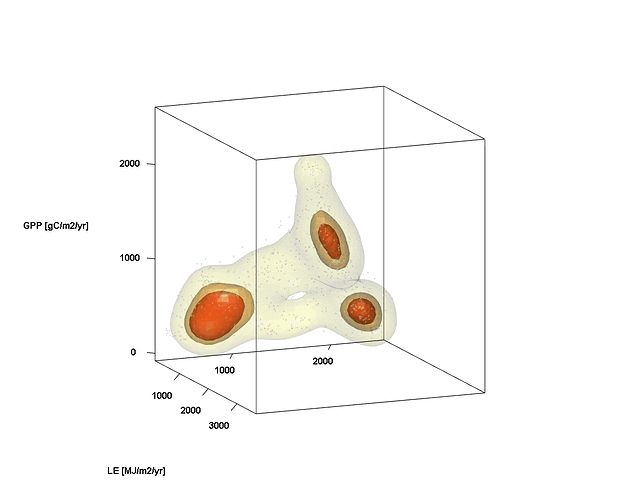
I want to plot something, that looks similar to this one below (some years ago with R):

Maybe it is just a matter of the settings in volume(algorithm=:iso,…). Or maybe one can do with surface, but I would not know how exactly. (still new to Julia).

Thanks for any help!

[raman_kumar]

Update 3D contours

[eldee]

Looking at the source code of contour:

function plot!(plot::Contour{<:Tuple{X, Y, Z, Vol}}) where {X, Y, Z, Vol}
    x, y, z, volume = plot[1:4]
    @extract plot (colormap, levels, linewidth, alpha)
    valuerange = lift(nan_extrema, plot, volume)
    cliprange = map((v, default) -> ifelse(v === automatic, default, v), plot, plot.colorrange, valuerange)
    cmap = lift(plot, colormap, levels, alpha, cliprange, valuerange) do _cmap, l, alpha, cliprange, vrange
        levels = to_levels(l, vrange)
        nlevels = length(levels)
        N = 50 * nlevels

        iso_eps = if haskey(plot, :isorange)
            plot.isorange[]
        else
            nlevels * ((vrange[2] - vrange[1]) / N) # TODO calculate this
        end
        cmap = to_colormap(_cmap)
        v_interval = cliprange[1] .. cliprange[2]
        # resample colormap and make the empty area between iso surfaces transparent
        map(1:N) do i
            i01 = (i - 1) / (N - 1)
            c = Makie.interpolated_getindex(cmap, i01)
            isoval = vrange[1] + (i01 * (vrange[2] - vrange[1]))
            line = reduce(levels, init = false) do v0, level
                isoval in v_interval || return false
                v0 || abs(level - isoval) <= iso_eps
            end
            RGBAf(Colors.color(c), line ? alpha : 0.0)
        end
    end

    return volume!(
        plot, Attributes(plot), x, y, z, volume, alpha = 1.0, # don't apply alpha 2 times
        algorithm = 7, colorrange = cliprange, colormap = cmap
    )
end

I guess the idea (for some reason, it seems quite inefficient) is that we check for ‘all’ values isoval between the minimum and maximum value of volume whether it lies sufficiently close (according to iso_eps) to one of the supplied levels. If so, we draw it using volume! (the source code of which I fail to locate) in a certain colour. (Now, in practice, we cannot check all possible values of course, so we restrict ourselves to a linear grid of N steps. If this grid is too coarse (for a given iso_eps), we might miss a certain level. Makie does not seem to supply any way to directly control N, but by supplying e.g. [0.1, 0.1, 0.1] instead of [0.1] for levels you do triple N. So getting a too coarse grid can be easily circumvented.)

Now suppose you would actually check all possible isovals. Then your shells would have a thickness of 2 * iso_eps. So we want to reduce iso_eps. But as far as I can tell, there’s currently no accessible way to do this. There are some hacky solutions possible though. I’m not fond of any of them as they constitute type piracy, but, hey, they do kind of work.

Overwrite Makie.plot!

Just increase 50 in the definition of N to e.g. 100:

using Makie: nan_extrema, automatic, to_levels, Colors

function Makie.plot!(plot::Contour{<:Tuple{X, Y, Z, Vol}}) where {X, Y, Z, Vol}
    x, y, z, volume = plot[1:4]
    @extract plot (colormap, levels, linewidth, alpha)
    valuerange = lift(nan_extrema, plot, volume)
    cliprange = map((v, default) -> ifelse(v === automatic, default, v), plot, plot.colorrange, valuerange)
    cmap = lift(plot, colormap, levels, alpha, cliprange, valuerange) do _cmap, l, alpha, cliprange, vrange
        levels = to_levels(l, vrange)
        nlevels = length(levels)
        N = 100 * nlevels

        iso_eps = if haskey(plot, :isorange)
            plot.isorange[]
        else
            nlevels * ((vrange[2] - vrange[1]) / N) # TODO calculate this
        end
        cmap = to_colormap(_cmap)
        v_interval = cliprange[1] .. cliprange[2]
        # resample colormap and make the empty area between iso surfaces transparent
        map(1:N) do i
            i01 = (i - 1) / (N - 1)
            c = Makie.interpolated_getindex(cmap, i01)
            isoval = vrange[1] + (i01 * (vrange[2] - vrange[1]))
            line = reduce(levels, init = false) do v0, level
                isoval in v_interval || return false
                v0 || abs(level - isoval) <= iso_eps
            end
            RGBAf(Colors.color(c), line ? alpha : 0.0)
        end
    end

    return volume!(
        plot, Attributes(plot), x, y, z, volume, alpha = 1.0, # don't apply alpha 2 times
        algorithm = 7, colorrange = cliprange, colormap = cmap
    )
end

'Add' isorange

(As a side note, snake case would make clearer we’re not talking about colours or fruits here .)

function Base.haskey(plot::Contour{<:Tuple{X, Y, Z, Vol}}, symb::Symbol) where {X, Y, Z, Vol}
    symb === :isorange && return true 
    invoke(haskey, Tuple{Plot, Symbol}, plot, symb)
end

function Base.getproperty(plot::Contour{<:Tuple{X, Y, Z, Vol}}, symb::Symbol) where {X, Y, Z, Vol}
    symb == :isorange && return 0.01
    return invoke(Base.getproperty, Tuple{Plot, Symbol}, plot, symb)
end

function new_iso_contour3d!(...)
   (...)
        contour!(...; levels=[lev, lev, lev], ...)
   (...)
end

Results, with alpha=1 for clarity:
(Before, overwriting Makie.plot!, ‘adding’ isorange)