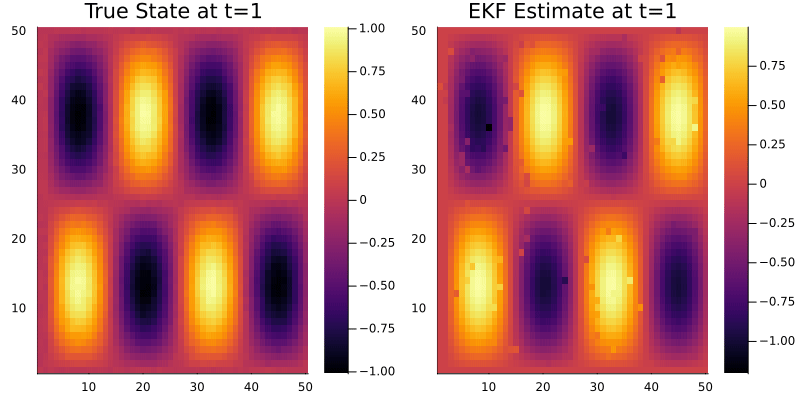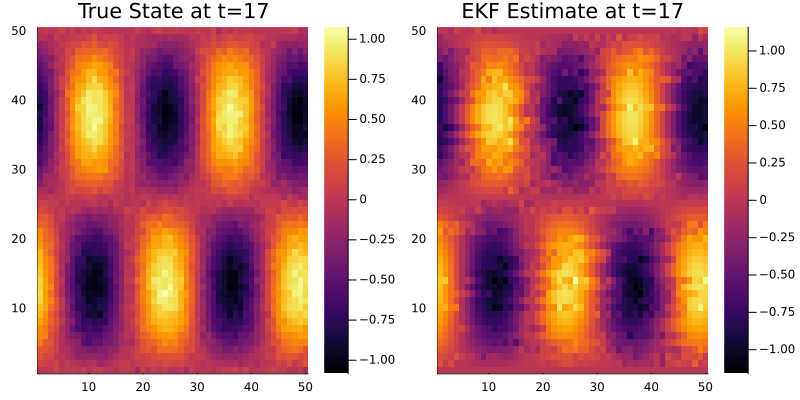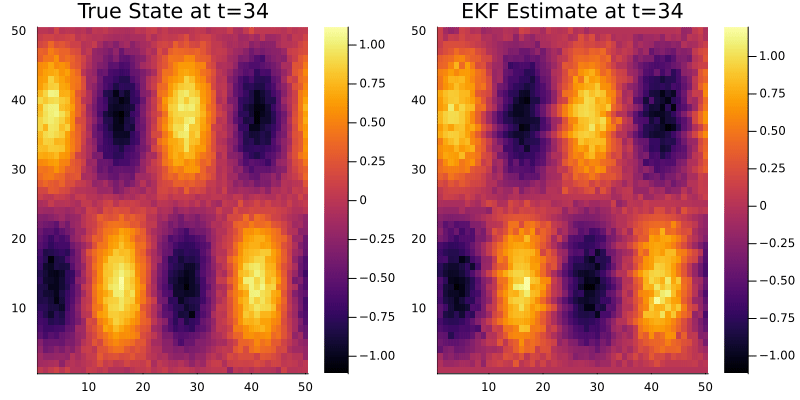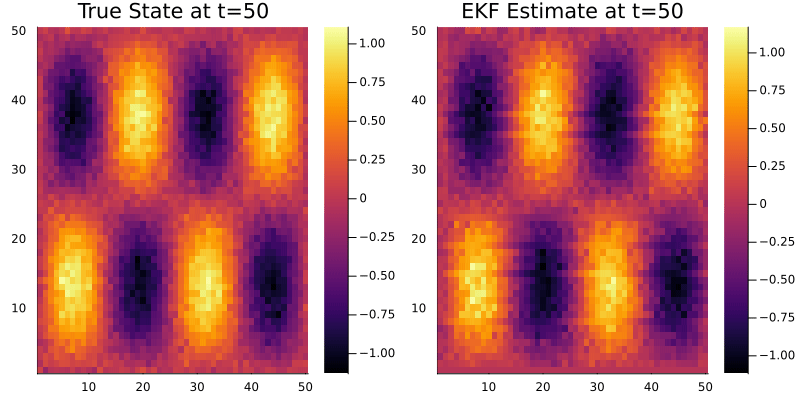
Hi everyone! I’m new to data assimilation and working with particle filters. I have a model where the β function is sinusoidal and linearly advects over time. It’s a 2D field on an 80×80 grid with double bumps.
I’m trying to use BootstrapFilter() for this setup, but I haven’t been able to get it working. I did manage to run the example provided in particleFilter.jl, but not beyond that.
Has anyone used BootstrapFilter() for 2D fields or something similar? Any tips or examples would be really helpful!
The below is the code provided as an example but seemingly its not for 2D.
using Distributions # For probability distributions
using Random
using DelimitedFiles
using ParticleFilters
using VegaLite
# === System Parameters ===
# timestep
const dt = 0.2
# system nonlinearity, higher the value, more non-linear the state is
const mu = 0.8
# standard deviation of the observation noise
const sigma = 0.6
# random number generator for reproducibility, Pseudorandom Number Generation:
# The Mersenne Twister is a pseudorandom number generator (PRNG), meaning it produces sequences of numbers that appear random but are actually generated by a deterministic algorithm
rng = MersenneTwister(1)
# x = [x1, x2]
# === System Dynamics Function used to generate true data with some error to show real- word error (can be replaced with forward model)===
function f(x, u, rng)
xdot = [x[2], mu * (1 - x[1]^2) * x[2] - x[1] + u + 0.01 * randn(rng)]
return x + dt * xdot
end
# observe only the first component x1 with gaussian noise.
# too high sigma will make the observation too noisy and hard to assimilate (particles spread out too much)
# === Observation Function which are the observation + some random value ===
function h(x, rng)
return x[1] + sigma * randn(rng)
end
# === Generate Synthetic Data ===
x = [3.0, 0.0] #initial state
k = 100 # number of time steps
xs = Array{typeof(x)}(undef, k) #stored true state trajectory
# exterbal control input
# in glacial model when the state is ice velocity, the control input is the subglacial water pressure or surface melt rate or external factors that affect the ice velocity
us = zeros(k)
ys = zeros(k) #noisy observations
for t in 1:k
global x
x = f(x, us[t], rng)
ys[t] = h(x, rng)
xs[t] = x
end
# true state trajectory
writedlm("x.txt", xs)
# observations
writedlm("y.txt", ys)
writedlm("u.txt", us)
println("✅ Data files written: x.txt, y.txt, u.txt")
# this gives weight to particles based on their match with observations
g(x1, u, x2, y) = pdf(Normal(sigma), y - x2[1])
ys = vec(readdlm("y.txt"))
us = vec(readdlm("u.txt"))
xmat = readdlm("x.txt")
n = 10_000
fil = BootstrapFilter(f, g, n)
# Unweighted particle belief consisting of equally important particles of type (___)
# uniform prior on x1 belongin to [-5, 5] (NOT GAUSSIAN DISTRIBUTION) and x2 = 0
# initial particle belief on state
b0 = ParticleCollection([[10.0 * (rand() - 0.2), 0.0] for _ in 1:n])
# println("✅ Initial particle cloud saved to initial_particles.svg")
# bs is the particle belief at each time step
# run the particle filter with the initial belief b0, control inputs us, and observations ys
# bs is a vector of ParticleCollection objects representing the particle beliefs at each time step
# each ParticleCollection contains particles representing the state of the system at that time step
bs = runfilter(fil, b0, us, ys)
# === Prepare Plotting Data ===
plot_data = [(; t, x1=x[1], x2=x[2], y, b_mean=mean(b)[1]) for (t, (x, y, b)) in enumerate(zip(eachslice(xmat; dims=1), ys, bs))]
println(plot_data)
# === Create Plot ===
plt = @vlplot(data=plot_data, width=700) +
@vlplot(:line, x=:t, y=:x1, color={datum="True State"}) +
@vlplot(:point, x=:t, y=:y, color={datum="Observation"}) +
@vlplot(:line, x=:t, y=:b_mean, color={datum="Mean Belief"})
# === Getting root mean squared error ===
# ...existing code...
# === Getting root mean squared error ===
rmse = [sqrt(mean((b_mean - x1)^2)) for (; x1, b_mean) in plot_data]
rmse_data = [(; t, rmse=rmse[t]) for t in 1:length(rmse)]
rmse_plot = @vlplot(data=rmse_data, width=700) +
@vlplot(:line, x=:t, y=:rmse, color={datum="RMSE"})
VegaLite.save("rmse.svg", rmse_plot)
println("✅ RMSE plot saved to rmse.svg")
VegaLite.save("myplot.svg", plt)
println("✅ Plot saved to myplot.pdf")
This example is running perfectly fine, but I’m not sure how to integrate my own 2D model with it. Below is my 2D model. To keep things simple, I’m using the analytical solution for linear advection to define the true model:
function generate_beta_field(grid::Grid, ω::Float64, t::Float64, v::Float64)
x_shifted = grid.xxh .- v * t
β = 1000 .+ 1000 .* sin.(ω .* x_shifted) .* sin.(ω .* grid.yyh)
return β
end
# ------------------------------------------------------
# Simulate true beta field over time
# ------------------------------------------------------
function simulate_beta_motion(grid::Grid, ω::Float64, v::Float64;
total_time::Float64=3600.0, dt::Float64=60.0)
nt = Int(total_time / dt) + 1 # Include time 0 and total_time
β_storage = Vector{Matrix{Float64}}()
for i in 0:nt-1 # Loop through time steps 0 to nt-1
t = i * dt
β_t = generate_beta_field(grid, ω, t, v)
push!(β_storage, β_t)
end
return β_storage
end
Also, I wanted to ask: is there another way I can perform particle filtering on this kind of model?
I came across the ParticleDA.jl package, which seems more general and supports things like multithreading and parallelization. But I’m not sure whether it’s possible (or advisable) to adapt it for my 2D analytical advection model. Has anyone tried using ParticleDA.jl with custom-defined models like this?
I’d love to hear if it’s flexible enough for such use cases, or if I should stick with writing a custom BootstrapFilter() pipeline from scratch.
Thanks in advance!