Parameter estimation in mathematical models of common functions (sine, cos, exp and other special functions)

[Geegee]

Hello all glad to have arrived here. I have recently picked up Julia, but am quite
excited about it!

I have many data sets that follow the same model but the parameters change widely from
dataset to dataset. In our labs we have python code that does the parameter estimation
for many of the models (lorentzian peaks, gaussian peaks, sine, exponential decay).

This seems to me a rather general problem so I always wondered why there isn’t a package
for this out there (at least in the python ecosphere I am not aware of one) and maybe in Julia there is also no such package.

Hopefully I just haven’t been able to find it. Nevertheless if this would be something
people are interested in then I could implement the code we use in our labs in a Julia package.

Best

[gdalle]

Hi, welcome to the community!
Parameter estimation is a very broad topic, and the Julia ecosystem has plenty of packages to do that. Perhaps if you gave some more detail on 1) the models you’re interested in and 2) the methods that your lab already uses, we could point you in the right direction.
For instance:

1. Are these statistical / physical / economic models? Do you have an explicit formula or just a simulator? Do they have hidden variables? How many parameters are involved?
2. Are the optimal parameters defined by an explicit formula, or an optimization problem? Do your Python procedures leverage differentiability or not? If so, first order or more? If not, do you use some kind of fitting heuristic?

etc. etc.

[Geegee]

Thanks for the nice welcoming.

@gdalle

r

I use the them model here but in effect we talk about continuous functions
like f(t; A, w) = A sin(wt), where we want to estimate A and w in often very noisy data.

Other functions we are interested in is lorentzian(s), exponential(s) - specifically decay, gaussian(s)

Our code leverages things like FFT, convolution, smoothing with gaussian filters and
a lot of heuristics to get to a decent parameter estimation (far from perfect).

[Tamas_Papp]

@Geegee

Our code leverages things like FFT, convolution, smoothing with gaussian filters and
a lot of heuristics to get to a decent parameter estimation (far from perfect).

You can probably find all of these ingredients in the Julia ecosystem, but your description above should answer

@Geegee

why there isn’t a package for this out there

: because you need to make a lot of decisions like this, so there is no general method for “estimation”.

That said, I am not sure why something simple like minimizing a sum of squared discrepancies would not work, but maybe your problem domain has something special.

If you want to get more specific help, post an MWE for generating the data, and the questions you have.

Please read: make it easier to help you

Welcome to the Julia Discourse! We are enthusiastic about helping Julia programmers, both beginner and experienced. This public service announcement (PSA) outlines best practices when asking for help. Following these points makes it easier for us to help you and more likely you’ll get a prompt, useful answer. Keywords are highlighted to make it easier to refer to specific points. Choose a descriptive title that captures the key part of your question, eg “plots with multiple axes” instead of …

[Geegee]

I get were you are coming from. Indeed whatever package someone would put together it would be extremely opinionated. Nevertheless I have the feeling that basically the same things are implemented again and again all over the world in different labs. Having robust estimators for the most common functions seems like a good thing to have, but I guess I am alone with this opinion, maybe indeed our code is so specialized that only we can use it.

I will do as you suggest and implement an estimator for the sine model as a start with the existing packages in Julia and when I get stuck post a MWE.

[Tamas_Papp]

@Geegee

I have the feeling that basically the same things are implemented again and again all over the world in different labs

The difficult parts are packaged as generic algorithms, eg an optimimizer (see Optimization.jl). Using it for estimation is a special case.

[Geegee]

This is where I struggle I feel. I don’t understand really what this package does. There is only the example of the Rosenbrock model where they try to find the minimum of a function if I understand correctly. I fail to make the connection to my problem. I think you mentioned this before that you could do estimation with optimizers but I have absolutely no glue how to do that. I see that the magic they do is in that they don’t get stuck in local minima and can cover huge “areas” in parameter space. I guess I need more examples with real world applications.
Especially how do I bring in the data in here? How does Optimization.jl relate to curve fitting i.e. LsqFit?

[Tamas_Papp]

@Geegee

I fail to make the connection to my problem.

A lot (but not all) of methodologies for estimation minimize some discrepancy between the data and a model, parametrizing the latter by the desired parameters, functional forms, etc. You can formalize this as least squares, maximum likelihood, etc.

@Geegee

I guess I need more examples with real world applications.

Or possibly some background in statistical procedures? Perhaps there is a mentor/advisor at your lab who knows the problem domain and could get you started.

[abraemer]

@Geegee

Especially how do I bring in the data in here? How does Optimization.jl relate to curve fitting i.e. LsqFit?

The connection is not that difficult to find. In curve fitting you ask “For which parameters does this function describe my data best?”. That sounds like an optimization, does it not?
How that works in practice is that you define some distance function that measures the distance between your model and your data. Then the process of fitting is just the minimization of that distance.

A very common method is “least squares”. Here the distance function is just the L_2 norm, i.e. d(x,y) = \sum_i |x_i - y_i|^2. Then you plug in your data points and the predictions of your model g(\theta)=d(\hat y, f(\hat x;\theta)), where f is the model function, \theta the model’s parameter, \hat x the measurement points and \hat y the measured values. Now minimizing g(\theta) is “fitting f to your data”.

[eteppo]

@Geegee

Especially how do I bring in the data in here? How does Optimization.jl relate to curve fitting i.e. LsqFit?

Think of the Rosenbrock example function as this “discrepancy function” which takes fixed values _p and optimizable parameters x. In your case the fixed values is your data, say x, y, and the discrepancy function is some measure of distance between model predictions and observed values, f(x, y, p) = model(x, p) - y. LsqFit.jl seems to implement its own algorithm (Levenberg–Marquardt) which perhaps works well specifically for least squares optimization of non-linear regression models.

[Geegee]

Thanks everyone for the helpful remarks. As someone with a physics background I probably used all the wrong terms and indeed upon thinking more about it I think what people commonly mean with parameter estimation is something I know as fitting. Whereas what i meant (falsly) is finding the initial bounds so my algorithm can find the best solution and not get stuck in local minima. In essence splitting the estimation part into two steps. One function which is tailored to the model used and another one which is generally good at finding the optimum.

I guess there probably is something in Optimize.jl for me but my feeling as suggested by @Tamas_Papp is that i would need to study a lot more optimal control theory, statistics or other related subjects.

[VinceNeede]

As a physics student and a self-taught in Julia myself, I can understand some struggles you may be encountering. Unfortunately I have not been able to understand what you mean either. If you are interested in finding the parameters A and w from a function f(x, A, w) = A sin(wt) that is a fitting problem. If the problem is with local minimums you can try to use a statistical optimizer, randomness can usually allow get out from local minima and go toward the global one.

If you could provide us a more specific and clear usage we might be able to help more.

[Tamas_Papp]

@Geegee

i would need to study a lot more optimal control theory,

Note that I have not suggested optimal control, which is probably irrelevant for your specific problem.

Whether you need more statistics or not depends, from your description of the problem you can get by with very little. Again, I think that the key difficulty here understanding what you are doing, which is not Julia-specific, and you would probably benefit from asking someone in your lab/university for help.

[Geegee]

Thanks a lot for the compassion .

One more thing that I probably didn’t clarify enough is our use case.
We measure data and want to extract from it the parameters (i.e. frequency)
but we know very very little about the parameters themselves in advance and we want
that all this happens unsupervised (automatically)
(like the frequency should be between 100e3 and 100e6, or the amplitude between 1 and 1e6).

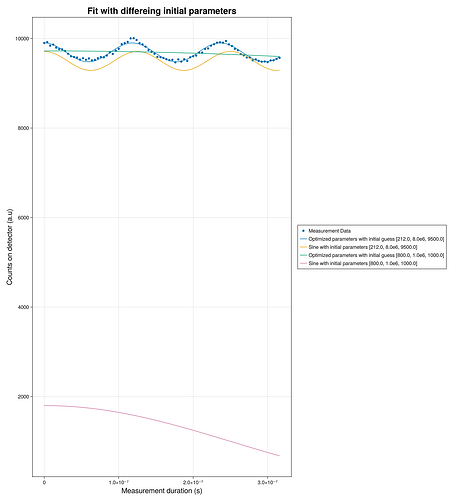
I put together a small example:

using DataFrames
using CSV
using LsqFit
using GLMakie

data = CSV.read("src/Data/estimation_mwe.csv", DataFrame)
axis = data[!, "axis"]
counts = data[!, "counts"]

function amp_cos_offset(t, p)
    p[1] * cos.(2 * π * p[2] * t) .+ p[3]
end

init_params1 = [212.0, 8.0e6, 9500.0]
init_params2 = [800.0, 1.0e6, 1000.0]

fit_res1 = curve_fit(amp_cos_offset, axis, counts, init_params1)
fit_res2 = curve_fit(amp_cos_offset, axis, counts, init_params2)

init_y1 = amp_cos_offset(axis, init_params1)
fit_y1 = amp_cos_offset(axis, fit_res1.param)
init_y2 = amp_cos_offset(axis, init_params2)
fit_y2 = amp_cos_offset(axis, fit_res2.param)
# visualize the fit results
f = Figure()
Axis(f[1, 1],
     title="Fit with differeing initial parameters",
     xlabel="Measurement duration (s)",
     ylabel="Counts on detector (a.u)",
     titlesize=25,
     xlabelsize=20,
     ylabelsize=20
     )

rd = scatter!(axis, counts);
l1 = lines!(axis, fit_y1);
l2 = lines!(axis, init_y1);
l3 = lines!(axis, fit_y2);
l4 = lines!(axis, init_y2);
Legend(f[1, 2], [rd, l1, l2, l3, l4],
    ["Measurement Data", "Optimized parameters with initial guess $init_params1",
        "Sine with initial parameters $init_params1", "Optimized parameters with initial guess $init_params2",
        "Sine with initial parameters $init_params2"])
f

I am not sure how to supply the raw data.
Also

@VinceNeede

If the problem is with local minimums you can try to use a statistical optimizer, randomness can usually allow get out from local minima and go toward the global one

this could be very interesting! If it helps I can also link the python code, that we use
to find the initial parameters (to start the optimization process).

[VinceNeede]

I think the best way would be to define a loss function and try to minimize that, for example you could use a ChiSq loss function. You would then have something like:

function find_opt_init_param(init_param)
    fit_result = curve_fit(amp_cos_offset, axis, counts, init_param)
    return sum(fit_result.resid .^ 2)
end

that you can then minimize with Optimization.jl.

If there is a lot of noise and it is very difficult to find some good starting parameters, you could bypass curve_fit and try some more “pure” Bayesian approach, you could then take a look at Turing.jl.

Needless to say that doing all this makes sense if you really have zero knowledge on the parameters and zero way to retrieve that (in the sinusoidal case, both amplitude and frequency can be estimated from the plot, or in physics most of the time you have some theoretical estimations, or at least some constrains)