How to model a chemical reaction network with changing parameters? (Catalyst.jl)

Specific Domains Chemistry
,
1

Hello,

I am hoping to model a chemical reaction network within a cell, where an organism may change the rate of a reaction given an external stimulus at time t. Is it possible to model a CRN wherea reaction constant, specified in rates changes at time t? Code pasted below.

using Catalyst
using Plots
using DifferentialEquations


rn = @reaction_network begin
    a, K --> RP + K
    b, RP --> P + RP
    (c, d), P + K <--> KP
    e, P --> 0
    f, RP --> 0
end a b c d e f

rates = (
    :a => 0.1,
    :b => 0.001,
    :c => 0.01,
    :d => 0.1,
    :e => 0.1,
    :f => 0.1
)
tspan = (0., 1000.)
u0 = [
    :K => 10,
    :RP => 0,
    :P => 0,
    :KP => 0
]

oprob = ODEProblem(rn, u0, tspan, rates)
solution = solve(oprob, Tsit5(), saveat=10.)

plot(solution)

Concretely, is it possible to generate a piecewise-like function in which the rate constant e changes values at a given time t?

Thank you!
Graeme

2

If there is a single change of rate at a know moment you could do something like this, where you change the value of a at t=1000 to 1.0
But probably there are more elegant solutions.

rates = (
    :a => 0.1,
    :b => 0.001,
    :c => 0.01,
    :d => 0.1,
    :e => 0.1,
    :f => 0.1
)
tspan = (0., 1000.)
u0 = [
    :K => 10,
    :RP => 0,
    :P => 0,
    :KP => 0
]

oprob = ODEProblem(rn, u0, tspan, rates)
solution = solve(oprob, Tsit5(), saveat=10.)

rates = (
    :a => 1,
    :b => 0.001,
    :c => 0.01,
    :d => 0.1,
    :e => 0.1,
    :f => 0.1
)
tspan = (1000., 2000.)
u0 = [
    :K => solution.u[end][1],
    :RP => solution.u[end][2],
    :P => solution.u[end][3],
    :KP => solution.u[end][4]
]

oprob = ODEProblem(rn, u0, tspan, rates)
solutionpart2 = solve(oprob, Tsit5(), saveat=10.)

and then combine the two solution parts

3

There are a bunch of ways to achieve this. Catalyst doesn’t support events yet, but you could explicitly convert rn to a ModelingToolkit ODESystem and pass in a symbolic event. You could also just add an event via the DifferentialEquations.jl interface, see here.

Finally, you could use a simple function for the rate expression to manually flip the rate at a specified time (note I then also set tstops in the call to solve to ensure the ODE solver steps to the switching time exactly):

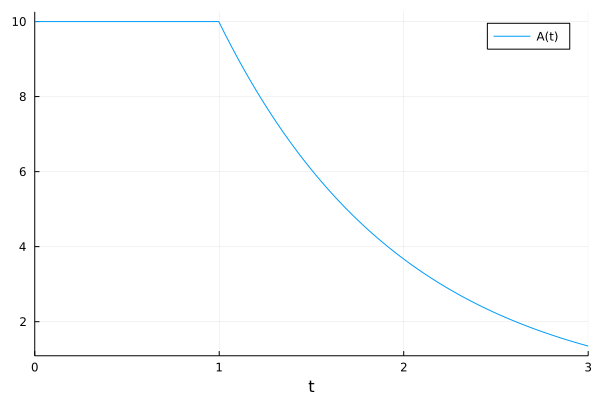
using Catalyst, OrdinaryDiffEq, Plots
rate(k1,k2,tswitch,t) = (t < tswitch) ? k1 : k2

# this ensures our custom function works with ModelingToolkit/Symbolics.jl
@register rate(k1,k2,tswitch,t)   

rn = @reaction_network begin
       rate(k1,k2,tswitch,t), A --> 0
       end k1 k2 tswitch
p = (:k1 => 0.0, :k2 => 1.0, :tswitch => 1.0)
u0 = [:A => 10.0]
tspan = (0.0,3.0)
oprob = ODEProblem(rn,u0,tspan,p)
sol = solve(oprob, Tsit5(), tstops=[1.0])
plot(sol)

giving
plot

4

And here is a version that uses IfElse.ifelse, and so probably works better in applications that might need AD:

using Catalyst, OrdinaryDiffEq, Plots, IfElse

rate(k1,k2,tswitch,t) = IfElse.ifelse(t < tswitch, k1, k2)

rn = @reaction_network begin
       rate(k1,k2,tswitch,t), A --> 0
       end k1 k2 tswitch
p = (:k1 => 0.0, :k2 => 1.0, :tswitch => 1.0)
u0 = [:A => 10.0]
tspan = (0.0,3.0)
oprob = ODEProblem(rn,u0,tspan,p)
sol = solve(oprob, Tsit5(), tstops=[1.0])
plot(sol)
1 Like
5

Fantastic. I ended up using IfElse, and it did what I needed. Thank you!

6

:+1: