How to get rid of noise in phase isosurface plots? Very short MWE included

Specific Domains Visualization
, , , ,
1

To keep it brief, I want to plot complex phase (angle) of a complex field. It seemed like Makie.jl’s contour or volume, should do the trick, but I get very noisy results for some reason?

using GLMakie

ph = [(r = hypot(x, y); ϕ = atan(x, y); angle(r*(r .- 5)*exp(1im*(2π*z/10 + ϕ)))) 
            for x in LinRange(-10, 10, 200), y in LinRange(-10, 10, 200), z in LinRange(-10, 10, 200)]

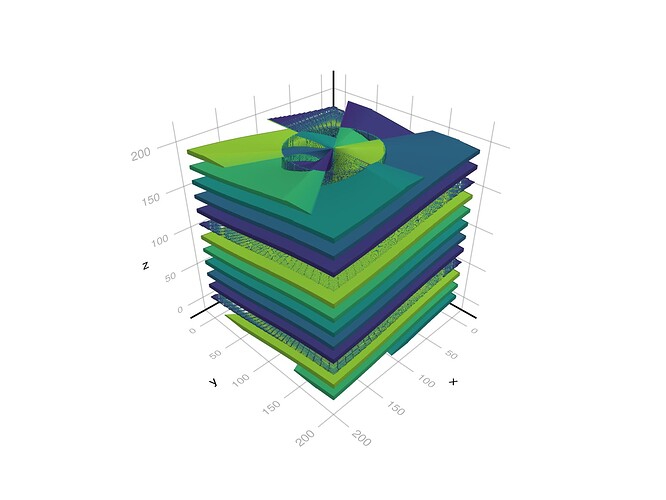
contour(ph)

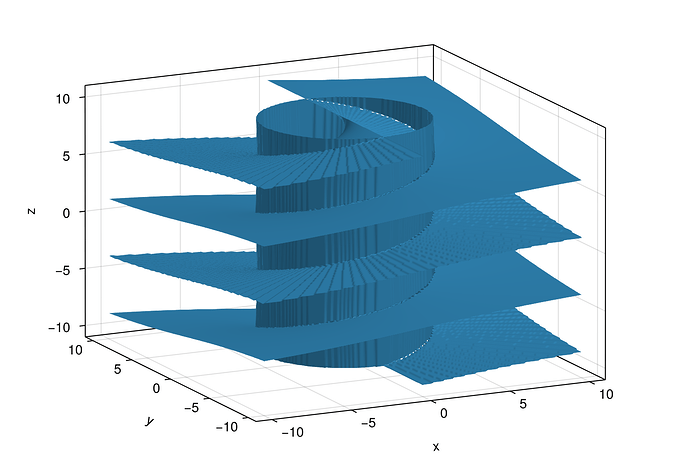
should yield something like

example
example1920×1440 78.6 KB

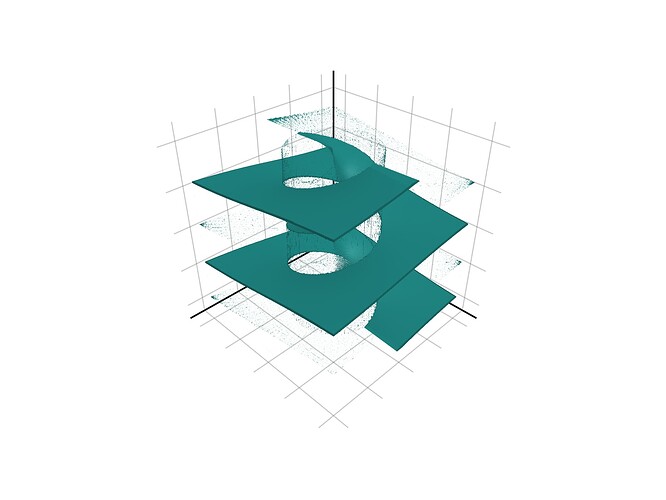
volume(ph, algorithm = :iso, isovalue = 0., isorange = 0.05)

yields

example2
example21920×1440 64.9 KB

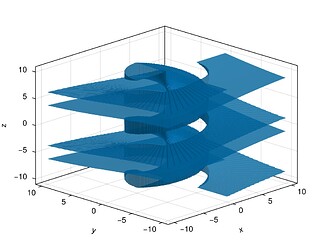
I don’t think this is an issue with the data. Filtering for a certain phase and then scattering

idxs_0 = filter(ijk -> -0.025 < ph[ijk...] < 0.025, 
                  collect(Iterators.product(1:200, 1:200, 1:200)))
scatter(idxs_0)

yields a clean plot…

example3
example31920×1440 172 KB

Does anyone have any experience in dealing with this issue?
Any suggestions on how to proceed are welcome!

2

have you tried setting a bigger isorange?

3

Yeah, I did. it doesn’t really help.

My guess is that this is an issue with the algorithm for generating/drawing the isosurface mesh. Based on examples in Makie’s documentation, I think there’s a built-in assumption about the domain being closed in some sense. Unlike here, where there are tears in the surface.

If you overlap the isosurface and the scatter plot you see that there’s no data where there is noise.

volume(ph, algorithm = :iso, isovalue = 0., isorange = 0.05)
scatter!(idxs_0, overdraw = true, markersize = 1., color = :red)
4

For plotting isosurfaces, I often have more luck using the MarchingCubes library:

using GLMakie
using MarchingCubes
using GeometryBasics

xs = ys = zs = LinRange(-10, 10, 200)
ph = [(r = hypot(x, y); ϕ = atan(x, y); angle(r*(r .- 5)*exp(1im*(2π*z/10 + ϕ)))) 
            for x in LinRange(-10, 10, 200), y in LinRange(-10, 10, 200), z in LinRange(-10, 10, 200)]
march_cube_data = MC(ph; x = xs , y = ys , z = zs)
march(march_cube_data, 0) # 0 is the isovalue
mc_mesh = MarchingCubes.makemesh(GeometryBasics, march_cube_data)

fig = Figure()
ax = Axis3(fig[1,1])
mesh!(ax, mc_mesh; backlight = 1.0)
fig

which yields:

iso_surface
iso_surface1458×982 218 KB

I’m not sure if you consider the middle cylinder to be noise, but since you have the expression (r-5) in your final expression and angle(0.0) is defined to be 0, I’m not sure how you would avoid it.

As a side-note, it took me a bit to parse that you have multiple expressions on one line separated by semicolons. Clearly it works, but I certainly would have found it easier to understand if it was written something like:

function calc_ph(x, y, z)
    r = hypot(x, y)
    ϕ = atan(x, y)
    ph = angle(r*(r .- 5)*exp(1im*(2π*z/10 + ϕ)))
    return ph
end
ph = [calc_ph(x, y, z) for x in xs, y in ys, z in zs]
5

Thank you! This is pretty much what I was hoping for! Also, no, I wouldn’t consider the center cylinder noise per-se, even though I’d prefer it not be there.

I am not very familiar with MarchingCubes, but I would imagine you could stop the cylinder from forming by imposing a maximum distance of points which are allowed to be joined. It also doesn’t form just for isovalue = 0. For

march(march_cube_data, π/2)

you get

pi_2
pi_21920×1440 94.4 KB

And, point taken, about the condensed block (r = hypot(x, y); ϕ = atan(x, y); angle(r*(r .- 5)*exp(1im*(2π*z/10 + ϕ)))). The reason I wrote it like this is because I was messing in the terminal and I absolutely hate to escape the return when editing begin end blocks. I always end up evaluating instead of inserting a new line. After I got it working, I just ended up pasting it here as I knew the code snippet worked.