Banded Jacobian of the constraints

Specific Domains Optimization (Mathematical)
,
1

Hello,
I am using JuMP for solving optimal control of a car on a track. I am trying to reformulate my problem, to improve the sparsity pattern of jacobian of constraints and Hessian of Lagrangian. I have managed to get the Hessian to nice form. For the query of Hessian and Lagrangian I am using this Computing Hessians · JuMP This is the Hessian:

julia> UnicodePlots.spy(H_star)
      ┌──────────────────────────────┐    
    1 │⣿⡻⢿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ > 0
      │⠛⠓⢰⣶⣶⣶⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ < 0
      │⠀⠀⢸⣿⣞⢝⣀⣀⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⢸⣿⣻⢿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠘⠛⠓⢱⣶⣶⣶⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣞⢝⣀⣀⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣻⢿⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠘⠛⠓⢱⣶⡶⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠸⠯⠾⢇⣀⣀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡿⣫⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠉⠉⢱⣶⡶⡆⠀⠀⠀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠸⠯⠾⢇⣀⣀⡀⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡿⣫⡇⠀⠀⠀│    
      │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠉⠉⢱⣶⡶⡆│    
   90 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠸⠯⠾⠇│    
      └──────────────────────────────┘    
      ⠀1⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀90⠀    
      ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀544 ≠ 0⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

But I am having trouble doing the same with jacobian. No matter how I reorder the constraints and variables, there are always multiple bands:

julia> UnicodePlots.spy(jacobian)
       ┌───────────┐    
     1 │⠛⠿⣷⣆⡀⠀⠀⠀⠀⠀⠀│ > 0
       │⠀⠀⠉⠛⣿⣧⣄⡀⠀⠀⠀│ < 0
       │⠀⠀⠀⠀⠀⠉⠹⢷⣶⣤⠀│    
       │⠀⠆⠦⣄⣀⡀⠀⠀⠘⠛⠋│    
       │⠀⣤⡄⠀⠀⠉⠉⠑⠐⠲⠤│    
       │⠀⠉⠛⠷⣦⣄⡀⠀⠀⠀⠀│    
       │⠀⠀⠀⠀⠀⠉⠙⠳⢶⣤⣀│    
       │⣣⠰⢂⠀⠀⠀⠀⠀⠀⠈⠉│    
       │⠀⠀⠈⠱⢂⠄⡀⠀⠀⠀⠀│    
       │⠀⠀⠀⠀⠀⠈⠁⠃⡤⣀⠀│    
       │⠄⠄⠄⠄⡀⡀⢀⢀⠀⠉⠚│    
       │⠈⢘⡐⠐⠐⠀⠆⠄⠌⠌⠄│    
       │⠊⠈⠰⢦⡀⠀⠀⠀⠀⠀⠀│    
       │⠀⠀⠀⠀⠐⠡⠂⡄⡀⠀⠀│    
   236 │⠀⠀⠀⠀⠀⠀⠀⠀⠉⠖⡠│    
       └───────────┘    
       ⠀1⠀⠀⠀⠀⠀⠀⠀⠀90⠀    
       ⠀⠀⠀968 ≠ 0⠀⠀⠀    

julia> list_of_constraint_types(model)
6-element Vector{Tuple{Type, Type}}:
 (NonlinearExpr, MathOptInterface.EqualTo{Float64})
 (NonlinearExpr, MathOptInterface.GreaterThan{Float64})
 (NonlinearExpr, MathOptInterface.LessThan{Float64})
 (AffExpr, MathOptInterface.EqualTo{Float64})
 (AffExpr, MathOptInterface.GreaterThan{Float64})
 (AffExpr, MathOptInterface.LessThan{Float64})

I am beginning to think, it has to do something with the constraints being different types.

Does it make sense to try to force them to be banded diagonal, or are they represented differently in memory and this is just a visualisation which has no impact? Could you please link me resources where this is explained?

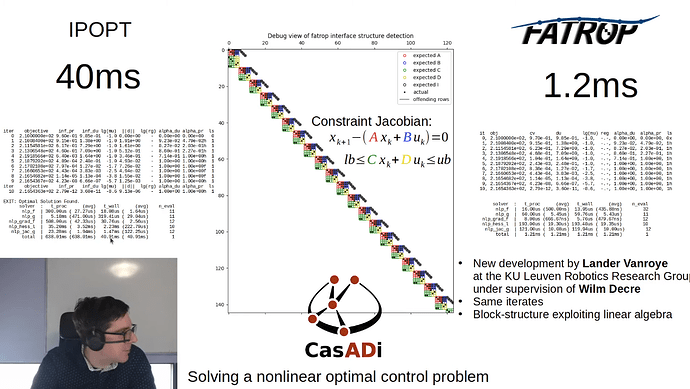
My goal is to try to get it looking similar to this video https://youtu.be/X-nS4i8jJyM?si=18TSLoxiMOP1IcBl&t=104

Screenshot_20251109_212325
Screenshot_20251109_2123251271×718 518 KB

Code which queries jacobian

using JuMP
import Ipopt
import LinearAlgebra
import Random
import SparseArrays
import MathOptInterface as MOI


function compute_optimal_jacobian(model::Model)
    rows = Any[]
    nlp = MOI.Nonlinear.Model()
    for (F, S) in list_of_constraint_types(model)
        for ci in all_constraints(model, F, S)
            if !(F <: VariableRef)
                push!(rows, ci)
                object = constraint_object(ci)
                MOI.Nonlinear.add_constraint(nlp, object.func, object.set)
            end
        end
    end
    MOI.Nonlinear.set_objective(nlp, objective_function(model))
    x = all_variables(model)
    backend = MOI.Nonlinear.SparseReverseMode()
    evaluator = MOI.Nonlinear.Evaluator(nlp, backend, index.(x))
    # Initialize the Jacobian
    MOI.initialize(evaluator, [:Jac])
    # Query the Jacobian structure
    sparsity = MOI.jacobian_structure(evaluator)
    I, J, V = first.(sparsity), last.(sparsity), zeros(length(sparsity))
    # Query the Jacobian values
    MOI.eval_constraint_jacobian(evaluator, V, value.(x))
    return SparseArrays.sparse(I, J, V, length(rows), length(x))
end

jacobian = compute_optimal_jacobian(model)

GLMakie.spy(reverse(jacobian,dims=1))
UnicodePlots.spy(jacobian)
2

Can you share the actual model? It might be useful for debugging.

I think internally JuMP.jl uses a single sparse matrix format, SparseMatrixCSC, whose performance shouldn’t be affected by permutations that make it look more or less banded. There are other matrix formats in the ecosystem (like BandedMatrices.jl) which can take advantage of bandedness, so if you compute the Hessian yourself you may be able to feed that back into a JuMP model. However, unless the underlying solver is pure Julia, I doubt it will impact performance either. Waiting for more competent people to answer though.

1 Like
3

Thanks for answer, I am computing the jacobian and hessian only for visualisation, for actual optimization I am relying on JuMP and IPOPT. The model is unfortunately spread across multiple files, so I don’t know how to share it more effectively than this link :confused:

The visualisation can be run by

include("src/experiments/singleTrackOpt.jl")

I will try to get minimal working example running and post it here

4

Hi @Ceserik,

JuMP doesn’t exploit any structure in the Jacobian or Hessian, so there’s little to be gained there.

We pass the sparsity pattern to Ipopt directly. In theory, you might be able to compile Ipopt with a linear solver that could exploit a particular sparsity pattern, but the default solver (MUMPS) doesn’t, and I don’t know of one off the top of my head that does.It looks like your screenshot talks about a custom linear solver.

About the order of the constraints: yes, JuMP orders constraints based on their type, and then by creation order within a type. There isn’t a way to have a custom order that mixes constraint types.

1 Like
5

Thanks for cleaning that up for me :slight_smile: .

1 Like