Von mises stress

[mary]

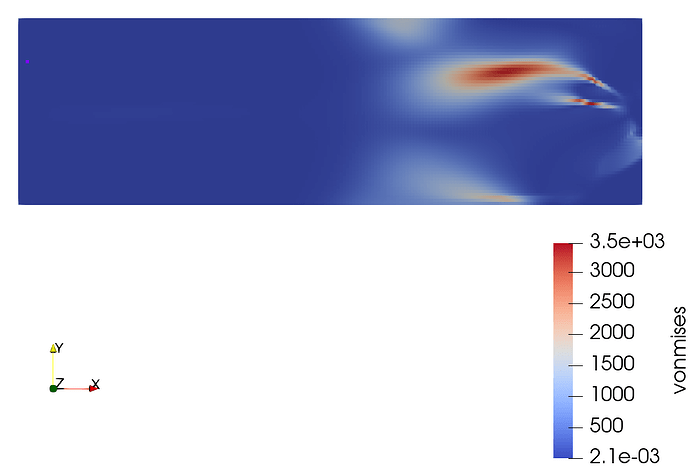
Hi, I am using gridap in julia to find the vonMises stress. As it is for topology optimization I penalized the E for material distribution. It is working correctly when I have unifor material distribution but it is not showing correct results when material distribution is not uniform

const  E_mat = 1.0
const  ν_mat = 0.3 
const  ηe = 1e-9
const  penal = 3

function  ElasFourthOrderConstTensor(E,ν,PlanarState)
    # 1 for  Plane  Stress  and 2 Plane  Strain  Condition
    if  PlanarState  == 1
        C1111 =E/(1-ν*ν)
        C1122 = (ν*E)/(1-ν*ν)
        C1112 = 0.0
        C2222 =E/(1-ν*ν)
        C2212 = 0.0
        C1212 =E/(2*(1+ν))
    elseif  PlanarState  == 2
        C1111 = (E*(1-ν*ν))/((1+ν)*(1-ν-2*ν*ν))
        C1122 = (ν*E)/(1-ν-2*ν*ν)
        C1112 = 0.0
        C2222 = (E*(1-ν))/(1-ν-2*ν*ν)
        C2212 = 0.0
        C1212 =E/(2*(1+ν))
    end
    C_ten = SymFourthOrderTensorValue(C1111 ,C1112 ,C1122 ,C1112 ,C1212 ,C2212 ,C1122 ,C2212 ,C2222)
    return   C_ten
end 
const C_mat = ElasFourthOrderConstTensor(E_mat ,ν_mat ,1)
function σfun(ε_in,pth)
        σ = (C_mat⊙ε_in)
    return  σ
    
end

function Em(p)
    Em = (ηe + (1-ηe)*(p ^ penal))
    return Em
end 
f = VectorValue(0,-0.125) 
function  stepDisp(fem_params,pth)
    A_Disp(u,v,pth) = ((p->Em(p))∘pth) * ε(v) ⊙ (σfun∘(ε(u),pth))
    a_Disp(u,v) = ∫(A_Disp(u,v,pth))fem_params.dΩ
    b_Disp(v) = ∫(v ⋅ f)fem_params.dΓ_Load
    op_Disp = AffineFEOperator(a_Disp ,b_Disp ,U_Disp ,fem_params.V0_Disp)
    uh_out = solve(op_Disp)
    return  uh_out
end 
I2 = SymTensorValue{2,Float64}(1.0 ,0.0 ,1.0)
I4 = I2⊗I2
I4_sym = one(SymFourthOrderTensorValue{2,Float64})
P_vol = (1.0/2)*I4
P_dev = I4_sym - P_vol
function σvon(ε_in,pth)
    
    σ = (C_mat⊙ε_in)
    von_dev = P_dev ⊙ σ
    j2 = 0.5*(von_dev ⊙ von_dev)
    von_stress = sqrt(3*j2)
    
    return von_stress
end
p0 = rand(fem_params.np)
pf_vec = pf_p0(p0; r, fem_params)
pfh = FEFunction(fem_params.Pf, pf_vec)
pth = (pf -> Threshold(pf; β, η)) ∘ pfh
uh = stepDisp(fem_params,pth)
von_stress = (σvon∘(ε(uh),pth))

this is the result

while there is almost no material in high stress region. graph below shows material distribution

I did my best to include most of the code. I appreciate your help.