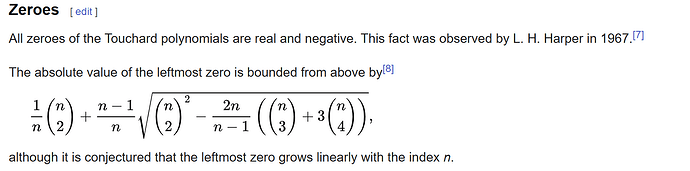Thanks a lot to everyone, i have working things now. However, from the begining the problem was not the right one, I am realizing now that the part of the curve I need to invert is not
f_n: \mathbb R_+ \to \mathbb R
but rather
f_n: [-\infty, x_n^*] \to \mathbb R_+ \text{ if n even, and } f_n: [-\infty, y_n^*] \to \mathbb R_- \text{ when n odd},
where x^* is the leftmost critical point of f_n, that is the leftmost root of its derivative.
Since f_n' = f_{n+1} / (x-1), that is the leftmost root of f_{n+1}. All roots of touchard’s polynomials are real and negatives.
Since this is the leftmost one, the part where i need to do the grid search is still monotonous so we are good. The issue is that I do not really know where is this leftmost root, even if wikipedia has a few hints.
Back to the drawing board I guess 
So Wikipedia gives a lower bound for the leftmost root :
So i guess that evaluating f_n at this lower bound would give a good starting point to look for the root. However, we should not go too far to the right and pass through the root, otherwise we are cooked (the function is not monotone there anymore). I will retry writing a solver.
Here is a piece of code that reimplements the inverse function that i needed. The interpolation is working correctly, even if there are a few artefacts.
and this is what i obtain after interpolation:
Current code
using Roots, Combinatorics, ApproxFun, Plots
function fₙ(x, ::Val{n}, s2::NTuple{n, Int}=ntuple(i->stirlings2(n, i), n)) where n
n==1 && return exp(x)
return x*evalpoly(x, s2) * exp(x)
end
function lower_bound_on_leftmost_root(::Val{n}) where n
n==2 && return - 1.0
n==3 && return - 1 / 0.380
n==4 && return - 1 / 0.216
n==5 && return - 1 / 0.145
n==6 && return - 1 / 0.106
n==7 && return - 1 / 0.082
n==8 && return - 1 / 0.066
n==9 && return - 1 / 0.055
n==10 && return - 1 / 0.046
C2 = binomial(n, 2)
C3 = binomial(n, 3)
C4 = binomial(n, 4)
term1 = C2 / n
discr = C2^2 - (2n / (n - 1)) * (C3 + 3*C4)
term2 = (n - 1)/n * sqrt(discr)
lower_bound = (term1 + term2)
return -lower_bound
end
leftmost_critical_point(::Val{n}) where n = lower_bound_on_leftmost_root(Val{n+1}())
starting_point(::Val{n}) where n = leftmost_critical_point(Val{n+1}())
last_summit(::Val{n}) where n = fₙ(leftmost_critical_point(Val{n}()), Val{n}())
function inv_fₙ(x, ::Val{n}) where n
n==1 && return log(x)
x₀ = starting_point(Val{n}())
return find_zero(
let s2 = ntuple(i->stirlings2(n, i), n)
t -> fₙ(t, Val{n}(), s2)-x
end,
x₀
)
end
N=3
x = -10:0.1:0
plot(x, fₙ.(x, Val{N}()))
lower_bound_on_leftmost_root(Val{N}())
leftmost_critical_point(Val{N}())
# The range of the inverse will be [summit,0] or [0,summit] depending on the usmmit sign (summit is neg is N is odd and pos is N is even i think)
last_summit(Val{N}())
starting_point(Val{N}())
inv_fₙ(-0.1, Val{N}())
N=1
s = last_summit(Val{N}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot(x, inv_fₙ.(x, Val{N}()), label="N=$N, truth")
# I think this one should be the lambert W function as f_1 = e^x * x IIRC.
N=2
s = last_summit(Val{N}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot!(x, inv_fₙ.(x, Val{N}()), label="N=$N, truth")
N=3
s = last_summit(Val{N}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot!(x, inv_fₙ.(x, Val{N}()), label="N=$N, truth")
N=4
s = last_summit(Val{N}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot!(x, inv_fₙ.(x, Val{N}()), label="N=$N, truth")
N=5
s = last_summit(Val{N}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot!(x, inv_fₙ.(x, Val{N}()), label="N=$N, truth")
function mkfun(::Val{n}) where n
s = last_summit(Val{n}())
I = s > 0 ? Interval(1e-4, s) : Interval(s, -1e-4)
return Fun(x -> inv_fₙ(x, Val{n}()), I)
end
inv_fns = (log, (mkfun(Val{k}()) for k in 2:5)...)
plot()
for (n, f) in enumerate(inv_fns)
s = last_summit(Val{n}())
x = sign(s) .* (1e-5:0.001:abs(s))
plot!(x, f.(x), label="N=$n, fitted")
end
plot!()
Does someone have an idea on how i could validate the result, and extract the polynomials from the objects to store them on disk somehow ?
![]()