Greetings, I’m a relatively new Julia user and have encountered a problem. I’m a bit embarrassed to post it here, since it seems sure to be something really obvious. A brief statement of the problem is as follows. I am trying to solve a second-order differential equation which depends on an external function. The final solution is to be found as a function of the arguments of this external function. I have tried to construct a minimal working example given below.
using Plots
using DifferentialEquations
f_p(t, p) = p[1]*sin(p[2]*t);
function rhs!(du, u, p, t)
du[1] = u[2]
du[2] = -u[1] + f_p(t,p)
end
function sol(x1, x2, T)
u0 = [0.1; 0.0]
tspan = (0, T)
p = [x1, x2]
prob = ODEProblem(rhs!, u0, tspan, p)
sol = solve(prob, save_idxs=1)
return sol
end
x1 = 0.8; x2 = 10.0;
plot(sol(x1, x2, 10.0), xlabel="t", ylabel="u(t)")
The above code encapsulates the essential features of the problem. The code above does produce a solution, but it seems to be wrong. I’d be grateful if anyone would give me a few hints regarding where I’m going wrong.
Thank you for reading.
How do you know it’s giving a wrong solution?
1 Like
I have compared the solution to one obtained in Mathematica, which shows a different plot.
Have you tried decreasing the tolerance? What’s the Mathematica code?
Changing the tolerance with abstol and reltol doesn’t seem to change anything. Or did you mean changing the tolerance in Mathematica?
The Mathematica code I used is given below (if that was what you were asking me to post?):
f[t_, x_, y_] := x*Sin[y*t]
s[x1_, x2_] :=
NDSolve[{u''[t] == -u[t] + f[t, x1, x2], u[0] == 0.1, u'[0] == 0},
u, {t, 0, 10}] // First
x1 = 0.8;
x2 = 10.0;
Plot[Evaluate[u'[t] /. s[x1, x2]], {t, 0, 10},
AxesLabel -> {"t", "u(t)"}]
This equation has an analytical solution
and the Julia solution very closely matches the analytical solution:
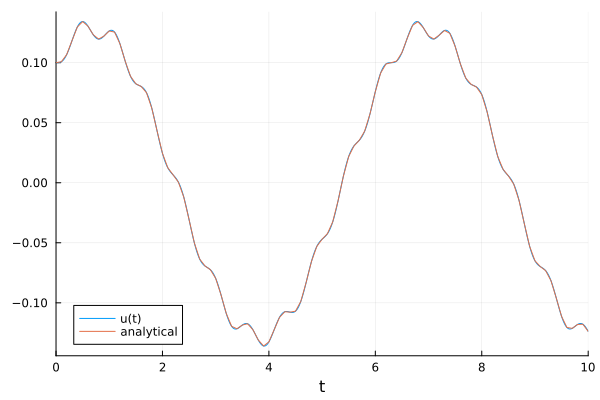
x1 = 0.8; x2 = 10.0;
plot(sol(x1, x2, 10.0), xlabel="t", label="u(t)")
analytical(t) = sin(t)*(-0.0444444cos(9t) - 0.0363636cos(11t) + 0.0808081) + (-0.0444444sin(9t) + 0.0363636*sin(11t) + 0.1)*cos(t)
plot!(0.0:0.1:10.0, analytical.(0.0:0.1:10.0), xlabel="t", label="analytical")
savefig("analyical_match.png")
So I’m curious what you’re getting from Mathematica because that is clearly the correct answer.
1 Like
Foolish of me not to check for an analytical solution. Peculiarly, the Mathematica code I attached yields a numerical solution which clearly does not match the analytical solution that Mathematica’s DSolve itself finds for the same equation. I see no option to attach a file to this reply, or I would have attached the pdf file of the plot. Nevertheless, the numerical solution obtained from Mathematica’s NDSolve appears to be oscillatory, but clearly different from from the analytical solution.
It seems Julia is finding the correct solution, so the premise of my original question is rendered null and void. One last question, if you do not mind. Is there any other “recommended” method to handle this kind of problems, other than the Julia code snippet I posted? I was able to find an example in the documentation of the package that had an external function, but it did not have other parameters on which the solution depended, so I was forced to take a different approach.
Thank you for taking the time to respond to this post, by the way. I’m very grateful.
4 Likes
Thank you for taking the time to respond!
1 Like
it may be worth pointing out that all functions (e.g. +) are external to your differential equation. user defined functions aren’t special.
Indeed, the only restriction seems to be that the user defined function be written in terms of (t, p) for it to be acceptable to DifferentialEquations.jl, if I understand correctly.
Sorry, you’re right, of course. It can also be written in terms of other parameters like (x1, x2), provided the values are supplied in the solver routine somewhere so that it evaluates to a numeric value, I think?
