I’d like to try different curves against data to see which of them would best fit. So in this example
x0 = collect(1.0:100.0)
y0 = x .^ 4.5
f0 = curve_fit(LinearFit, x0, y0)
I’d like to learn just how bad it is, but is there an easy way to get that out of it?
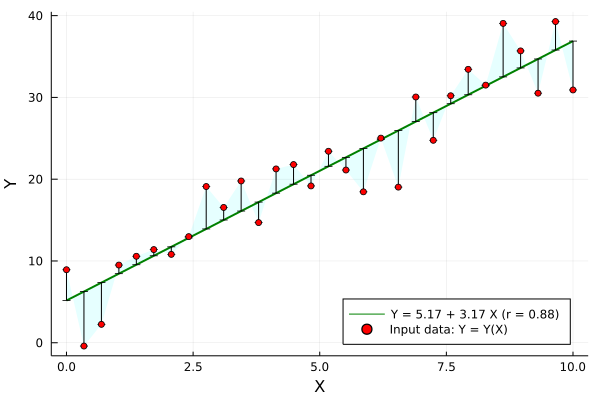
Just in case it might be useful, sharing one linear regression example below, where the correlation coefficient r is displayed and other regression statistics are computed too:
using Plots, Random, Distributions, GLM, DataFrames, Printf
# input data
n = 30
x = LinRange(0,1, n) .* 10
e = rand(Normal(0,mean(x)/4),n)
parms = Dict(:b0 => 6, :b1 => 3.2)
y = parms[:b0] .+ parms[:b1] .* x .+ 3*e
data = DataFrame(X=x, Y=y)
# linear regression
ols = lm(@formula(Y ~ 1 + X), data)
a, b = coef(ols)
r = r2(ols)
# plotting
yhat = parms[:b0] .+ parms[:b1] .* x
err = y - yhat; z0 = 0*err;
str = "Y = " * @sprintf("%.2f",a) * " + " * @sprintf("%.2f",b) * " X (r = " * @sprintf("%.2f",r) * ")"
plot(x,yhat, label=str, lw=2, c=:green, yerror=(z0,err), ribbon=(z0,err), fc=:cyan, fa=0.1)
scatter!(x, y, mc=:red, xlabel="X", ylabel="Y", label="Input data: Y = Y(X)", legend=:bottomright)
Some stats output after command:
julia> ols = lm(@formula(Y ~ 1 + X), data)
Y ~ 1 + X
Coefficients:
───────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
───────────────────────────────────────────────────────────────────────
(Intercept) 5.16706 1.31032 3.94 0.0005 2.48298 7.85113
X 3.172 0.225023 14.10 <1e-13 2.71106 3.63294
Thanks, I’ll look into these examples. The problem itself should be relatively simple, the actual data is a straight line in a log-log plot, it’s just not quite that easy to post its code here. (The wikipedia page for log-log plots is also somewhat opaque.)
I have a very simple package to make fits really, really simple, in common cases: GitHub - m3g/EasyFit.jl: Easy interface for obtaining fits for 2D data
Just for fun:
To fit a polynom you can use
"""
Fit y = f(x) to nth order polynomial.
Returns list of polynomial coefficients.
"""
function polyfit(x,y,n)
@assert length(x) > n
A = [k^n for k in x, n in 0:n]
A\y
end
To reason about the fit you would need to look for measures often found under goodness of fit, but I am not sure which are implemented by julia packages. If you want to look into one of those methods I think the package HypothesisTests is a good resource.
Also if you try to fit a log transformed exponential function you should use a weighted least square fit to compensate for the transform.
I got this working with minimal effort (on the package side, I had some other unrelated Julia problems though). When I take log10 of the original x and y values, and do fit = fitlinear(x_log,y_log), I get a nice match.
------------------- Linear Fit -------------
Equation: y = ax + b
With: a = -0.9999071242153111
b = 5.319512210970783e-5
Pearson correlation coefficient, R = 0.9999734052571524
Average square residue = 9.731441862500589e-6
Predicted Y: ypred = [2.999774567768043, 2.6987725305011243...
residues = [-0.0008626824944601985, -0.007119649365998182...
--------------------------------------------
When I tried to fit against the original (non-log) data, the only one that gave good results was fit = fitspline(x,y).
-------- Spline fit ---------------------------
x spline: x = [0.001, 0.011...
y spline: y = [1005.2007999999998, 90.34990000000002...
-----------------------------------------------
A spline will always look well, but you cannot use them to really get any information about your data.
If your x and y values are related by something like y = A/x it is expected that the log/log plot is linear (log(y) = A - log(x)) while the plot of the original data is not.
Yes. X ^ -1 is close. Can I fit that with EasyFit?
No, I didn’t implement that (you can fit anything using directly LsqFit). Although the approach of fitting a straight line in the log/log plot is the best approach. Linear fits are always better.
LsqFit seems to be more general and conveniently provides the confidence intervals for the parameters estimated.
A correlation coefficient might also be obtained from the approximation of the covariance matrix. An attempt below, r formula to be confirmed.
PS: in your case it is possible and better to work with a log-log scale.
using LsqFit, Plots, Printf
# input noisy data
t = 0.01:0.01:1
y = 420*t.^(-0.13 .+ 0.02*rand(length(t)))
# LsqFit
m(t, p) = p[1] * t.^(-p[2])
p0 = [0.5, 0.5]
fit = curve_fit(m, t, y, p0)
# fit parameters and confidence interval
p = fit.param
confidence_interval(fit, 0.1) # 10% confidence intervals
# correlation coefficient = covariance of 2 variables / product of their standard deviations
cov = estimate_covar(fit)
r = cov[1,2]/sqrt(cov[1,1]*cov[2,2]) # TODO: confirm formula
# plot results
str = @sprintf("%.1f",p[1])*"*t^(-" * @sprintf("%.3f",p[2]) * ")" * @sprintf("; r ~ %.2f",r)
scatter(t,y, mc=:reds, ms=3, xlabel="t", label="input data")
plot!(t,m(t,fit.param),ly=0.25,lc=:blue, ylabel="y(t)", label="LsqFit: "*str)
julia> p = fit.param
419.2404632519413
0.12214587254371537
julia> confidence_interval(fit, 0.1) # 10% confidence intervals
(418.14933388256867, 420.331592621314)
(0.12055572549189375, 0.12373601959553698)
julia> r = cov[1,2]/sqrt(cov[1,1]*cov[2,2]) # TODO: confirm formula
-0.7431633567883187
After thinking about this, I agree. The linear plot is really hard to read if you want any useful info out of it. The only reason against the log-log plot is that I’m not so used to such plots. Well, time to learn.
I’ll take a look at the solutions a bit later.
Also, if this was a part of a machine learning problem, trying gradient descent on the linear data would be a lost cause. I ’knew’ that already, but visualizing it makes is clearer.
If you can linearize the plot, you probably should do the linear fit and afterwards recover the non-linear parameters from that fit.
Now, how you maybe using this for optimizing anything is another story. The function 1/x is also minimum at x -> infty, thus minimizing it or the linearized version will take you to the same place.
How would I get the lin-lin equation from this log-log fit? I spent some reading of the wikipedia page, but not enough to fully get it.
Ok, got it. To change from log-log to lin-lin one can do:
y₂ = MathConstants.e .^ ( a .* log.(x) .+ b .* log.(10))
I did use WolframAlpha, I fed it log10(y) = a * log10(x) + b
It says the answer is approximate form. I then changed it to Julia form.
log₁₀y == a * log₁₀x + b
10 ^ log₁₀y == 10 ^ ( a * log₁₀x + b )
y == 10 ^ ( a * log₁₀x + b )
y == 10 ^ ( a * log₁₀x ) * 10 ^ b
magic..
y == MathConstants.e .^ ( a .* log.(x) .+ b .* log.(10))
Above is pseudo-code.
Indeed. That can be written in Julia as:
y2 = exp(fit.b) * x.^fit.a
(where fit.b and fit.a are the intercept and slope of the linear fit of the log-log plot - with base e. If you use base 10, use log10, and then y_2 = 10^{fit.b} x^{fit.a}.