As a follow up to my previous post and a response to @RoyiAvital’s message to me, here’s a way to do Proportional Navigation.
using Plots, DifferentialEquations, LinearAlgebra
##
# Parameters
N = 5.0
# Target:
r⃗ₜ(t) = [ cos(t); sin(t); 0]
v⃗ₜ(t) = [-sin(t); cos(t); 0] # TODO: derive automatically?
#Define the problem
function propnav(a⃗ₘ, v⃗ₘ, r⃗ₘ, N, t)
R⃗ = r⃗ₜ(t) - r⃗ₘ # displacement vector from missle to target
v⃗ₚ = v⃗ₜ(t) - v⃗ₘ # relative velocity from missle to target
Ω⃗ = (R⃗ × v⃗ₚ) ./ (R⃗⋅R⃗) # rotation vector
a⃗ₘ .= -N * norm(v⃗ₚ) * cross((R⃗ / norm(R⃗)), Ω⃗)
end
#Initial Conditions
x₀ = [0.0, 0.0, 0.0]
dx₀ = [1.0, 0.0, 0.0]
tspan = (0.0, 1.0)
#Pass to solvers
prob = SecondOrderODEProblem(propnav, dx₀, x₀, tspan, N)
sol = solve(prob, Tsit5(), saveat=0.01)
#Plot
missledata = hcat(sol.u...)'
v⃗ₘx = missledata[:,1]
v⃗ₘy = missledata[:,2]
v⃗ₘz = missledata[:,3]
r⃗ₘx = missledata[:,4]
r⃗ₘy = missledata[:,5]
r⃗ₘz = missledata[:,6]
targetpath = hcat(r⃗ₜ.(sol.t)...)'
r⃗ₜx = targetpath[:,1]
r⃗ₜy = targetpath[:,2]
plot( r⃗ₜx, r⃗ₜy, lw = 5.0 .* sol.t, label="Target")
plot!(r⃗ₘx, r⃗ₘy, lw = 5.0 .* sol.t, label="Missile")
##
@userplot PursuitPlot
@recipe function f(cp::PursuitPlot)
t, x, y, i = cp.args
n = length(x)
linewidth --> range(0.75, 10, length = i)
aspect_ratio --> 1
x[1:i], y[1:i]
end
n = length(sol.t)
anim = @animate for i ∈ 2:n
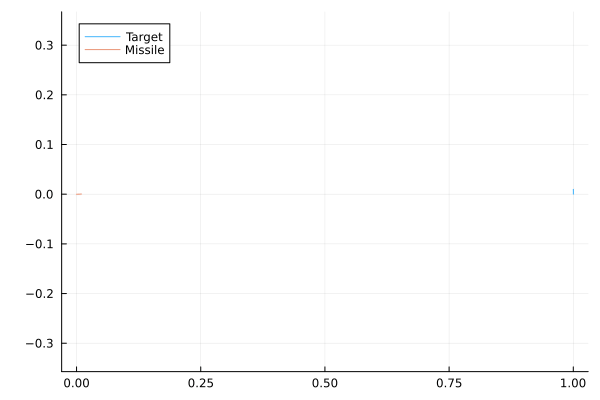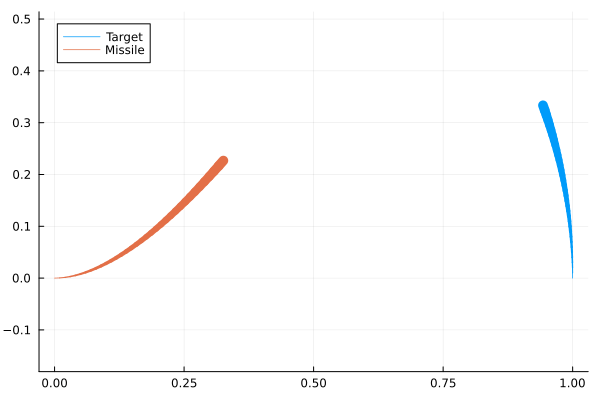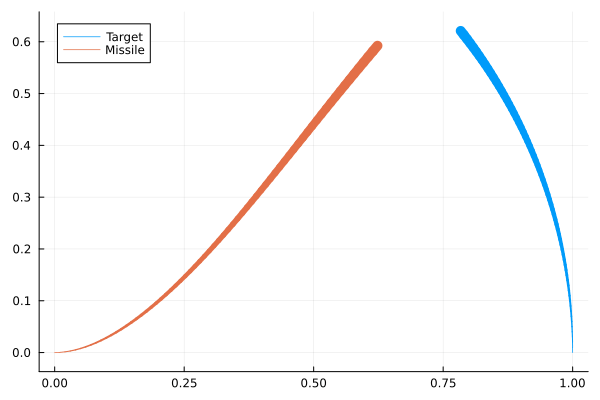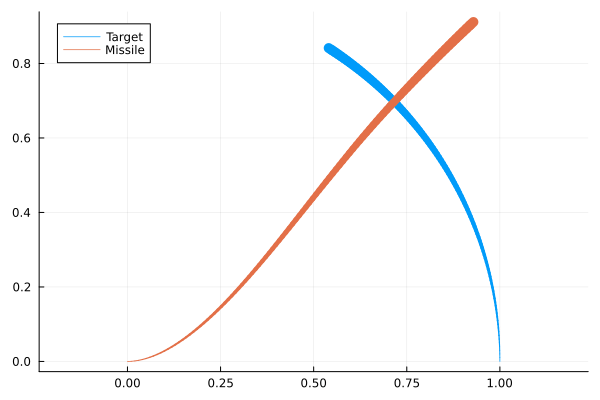
pursuitplot(sol.t, r⃗ₜx, r⃗ₜy, i, label="Target")
pursuitplot!(sol.t, r⃗ₘx, r⃗ₘy, i, label="Missile")
plot!(leg=:topleft)
end
gif(anim, "test.gif", fps = 15)
I’m sure there’s a more elegant way to do this but it’s at least a start. I noticed some solvers struggle with instability at the time where the missile and target would collide which makes sense.