Reparametrized Beta(μ, σ²) in Turing: how to set a prior that depends on another parameter?

Specific Domains Probabilistic programming
1

I am trying to model data between ]0, 1[ using Bayesian regressions in Turing.

It is fairly common to use a Mean/Variance parametrization to the Beta (see Wikipedia), allowing to express priors on intuitive quantities. This is the default Beta parametrization used in R’s brms (see this explanation)

Here is my MeanVarBeta wrapper:

using Turing, Distributions, Random

# Reparameterized Beta distribution
function MeanVarBeta(μ, σ²)
    if σ² <= 0 || σ² >= μ * (1 - μ)
        error("Variance σ² must be in the interval (0, μ*(1-μ)=$(μ*(1-μ))).")
    end

    ν = μ * (1 - μ) / σ² - 1
    α = μ * ν
    β = (1 - μ) * ν

    return Beta(α, β)
end
  • My first question is: is this reparametrized Beta already implemented in a package (I didn’t see it in Distributions)? To make sure it’s correct and so that I don’t want to reinvent the wheel.

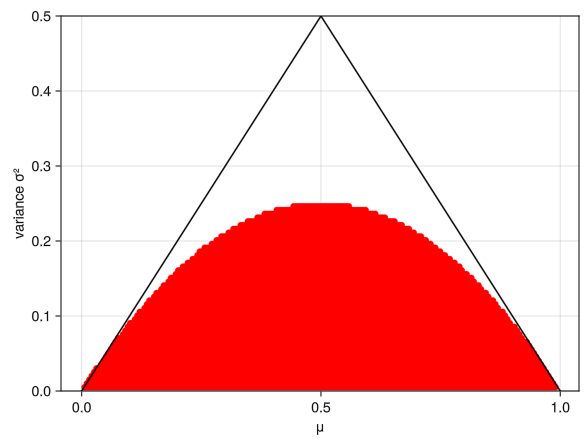
The key issue is that this distribution’s parameters depend on one another (var must be < μ*(1-μ). In red are the possible joint parameter space:

image

Here’s a potential Turing Beta reg model:

@model function model_Beta(x)
    μ ~ truncated(Beta(1,1), 0.3, 0.7)
    σ ~ Uniform(0.05, 0.15)
    x = MeanVarBeta(μ, σ)
end
chains = sample(model_Beta(rand(MeanVarBeta(0.5, 0.1), 100)), NUTS(), 300)

As you can see, I had to be very strict with the priors to avoid exploring the space where it errors (when var > μ*(1-μ)).

  • My second question is: how can we specify the priors / the model to avoid exploring the parameter space conditionally on another prior parameter?
2

For the latter question, does σ ~ Uniform(esp(typeof(μ)), μ * (1 - μ) - esp(typeof(μ))) solve the problem? Priors of one parameter can depend on another, and if the prior is zero in the forbidden region then that should never get explored.

3

That looks like exactly what we’d need, thanks!
But I’m having trouble understanding what for are esp() and typeof(), and I didn’t find much documentation on conditional prior parameters on google :confused:

Do you know if this syntax is described somewhere or not yet?

4

Oh sorry, first of all I had a typo, it should say eps rather than esp. Second, that’s all unnecessary fanciness, eps(typeof(μ)) gets the smallest magnitude number representable using the type of the variable μ. Most probably μ is a 64bit floating point number, in which case eps(typeof(μ)) is roughtly 2.2e-16. Uniform(eps(typeof(μ)), μ * (1 - μ) - eps(typeof(μ))) is essentially just Uniform(0, μ * (1 - μ)), except both of the ends are moved a tiny bit to avoid the problematic end points of the interval.

2 Likes
5

Thanks a lot it’s all clear now (and it works :slight_smile:)

Here’s the full model if others are interested:

using Turing, Distributions, Random

# Reparameterized Beta distribution
function MeanVarBeta(μ, σ²)
    if σ² <= 0 || σ² >= μ * (1 - μ)
        error("Variance σ² must be in the interval (0, μ*(1-μ)=$(μ*(1-μ))).")
    end

    ν = μ * (1 - μ) / σ² - 1
    α = μ * ν
    β = (1 - μ) * ν

    return Beta(α, β)
end

@model function model_Beta(x)
    μ ~ Beta(1, 1)
    σ ~ Uniform(eps(typeof(μ)), μ * (1 - μ) - eps(typeof(μ)))
    for i in 1:length(x)
        x[i] ~ MeanVarBeta(μ, σ)
    end
end
chains = sample(model_Beta(rand(MeanVarBeta(0.5, 0.2), 200)), NUTS(), 500; 
   initial_params=[0.5, 0.1])
2 Likes