Problem solving ODE for long tspans

New to Julia
1

Hello there,

I’m student of Orbital Dynamics and Planetary Dynamics and i am trying to write a program in JULIA similar to the one i have in FORTRAN. In general everything is working as it should, however in some cases my t_spans are quite long and could be thousands of years (or a million of years), in this type of situation I’m used to using adaptive step integrators quite used in astronomy like Bulirsch–Stoer but in the DifferentialEquations library there is no BS implemented.

I’m having difficulties with reaching a maximum number of iterations and with the integration time when I increase the maxiters to 1e9 to obtain what i want.

Any tips or possible solution that can help me in this situation ?

1 Like
2

(a) Bulirsch–Stoer is a terrible method that is not suitable for long time spans in an efficient way and is only used because someone who didn’t know anything about differential equation solvers wrote a book telling people to use it, and (b) there are many different extrapolation methods implemented in the library.

https://diffeq.sciml.ai/stable/solvers/ode_solve/#Parallelized-Explicit-Extrapolation-Methods

ExtrapolationMidpointHairerWanner or ExtrapolationMidpointDeuflhard with the :bulirsch sequence is a GBS method. But again, it’s probably not a good idea in most scenarios unless you have a high core count and use the threading option. Otherwise something like Vern9 is usually better.

4 Likes
3

I see. Thanks for the enlightenment, sometimes I end up using things as “black boxes”

At the moment I’m testing several algorithms like Vern9() and they all seem to be more efficient in a matter of time than the BS.

I’m doing some tests on a simple problem like the planar restricted three body problem, but even though Vern9 is quite efficient in this case limits me to have an abstol = 1e-16 which ends up using a lot of memory due to the amount of allocations that are needed. I’m trying to optimize the algorithm to avoid high memory usage.

Thank you.

4

Did you turn off saving to just what you need?

That’s floating point accuracy (if relative to 1). Just change to different floating point types if you need more.

5

Yes I’m saving 2500 points to check if the orbits is fine. Sometimes I just need the last point than I save the last point.

I tried to use StaticArrays however i’m not sure what i was doing wrong or if it’s even possible use in systems like this.

In that case i’m solving the CR3BP equations with the variational equations and a chaotic indicator

For 5e3 periods of my orbit i’m getting 2.47GB memory usage avg

image
image923×180 4.39 KB

For 5e4 periods its 24.6GB
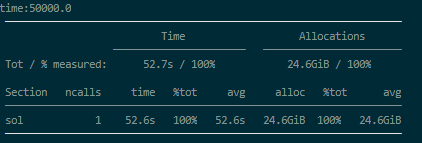
image

Perhabs its already maximum optimized but i’m not sure. i’ll share my code down there.

using Plots, LinearAlgebra, Random, DataFrames, TimerOutputs, StaticArrays, DifferentialEquations

const to = TimerOutput()

@inline @inbounds function vy0(C,p,v)
   """
   Calculate Vy0 from jacobian value
   input : (C,p,v) ...
            C = Jacobi cte
            v = x,y,vx
            p = mass ratio parameters mu
   """
       #cartesian coordinates
       x, y, x̂= v
       #distance vectors
       r1 = ((x+μ)^2 + y^2)^(1/2)
       r2 = ((1-x-μ)^2 + y^2)^(1/2)
       #jacobi integral - constant C.
       ŷ = (x^2 + y^2 - x̂^2 + 2*((1-μ)/r1 + μ/r2) - C)^(1/2)
       return ŷ
end



"""
Initial Conditions
"""
global μ = 0.01 # mass ratio binary main system

# third body
CJ = 0 # Jacobi cte
x0 = 1.893
y0 = 0
vx0 = 0
vyu = -vy0(CJ,μ,[x0,y0,vx0]) #sign negative for retrograde orbits



"""
Create a random set of tangent vector for MEGNO
Get normalized vectors for MEGNO
"""
rng = MersenneTwister(234);
a1 = rand!(rng, zeros(4))
global dd = 0
for i in 1:length(a1)
	if a1[i] <= 0.5
		a1[i] = -a1[i]
	end
end
for i in 1:length(a1)
	global dd += a1[i]^2

end
dd = sqrt(dd)
for i in 1:length(a1)
a1[i]= a1[i]/dd
global dd += a1[i]^2
end


####################
"""
u0 state vector = [x0,y0,vx0,vy0,xrng,yrng,vxrng,vyrng,megno_mean,megno_final]
x0,y0,vx0,vy0 -> Third body

%%%% MEGNO - REFERENCE : https://www.aanda.org/articles/aa/pdf/2001/41/aah2931.pdf
xrng,yrng,vxrng,vyrng = random initial conditions to calculate megno with variational equations
megno_mean = mean value of (dot var_equations / var_equations)
megno_final = numerical integration of the MEGNO mean value
"""
u0 = [x0, y0, vx0, vyu, a1[1], a1[2], a1[3], a1[4], 0.0, 0.0] # vector with initial conditions
println("Initial state vector :",u0)
println("JacobiCte Initial :",CJ)
# Time Span
t_end = 2*pi*5e4
tspan=(0.0,t_end)
numberofpoints = 2500


@inline @inbounds function cr3bp_rhs(du,u,μ,t)
"""
Planar Circular Restricted 3body problem
Equations of motion in co-rotating frame

	in:
		u = position and velocities of the particle
		μ = mass ratio parameter == μ2
		t = time span
	out:
		du = integration of the acel. and vel.

"""

	#cartesian coordinates

	r1 = ((u[1] + μ)^2 + u[2]^2)^(1/2)
    r2 = ((-1 + u[1] + μ)^2 + u[2]^2)^(1/2)

	du[1] = u[3] # F1
    du[2] = u[4] # F2
    du[3] =  2*u[4]  + u[1] - (1 - μ)*(μ + u[1])/(r1^3) - μ*(-1 + μ + u[1])/(r2^3) # F3
    du[4] = -2*u[3]  + u[2] - (1 - μ)*u[2]/(r1^3)       - μ*u[2]/(r2^3) # F4

	# renormalizing tangent vectors everystep for MEGNO - Chaotic Indicator
	normvec = sqrt(u[5]^2 + u[6]^2 + u[7]^2 + u[8]^2)
	xm = u[5]/normvec
	ym = u[6]/normvec
	vym = u[7]/normvec
	vxm = u[8]/normvec

	# mass parameters 
	mu1 = 1 - μ
	mu2 = μ
	#derivatives f3
	df3x = 1.0-mu1/r1^3-mu2/r2^3+3.0*mu1*(u[1]+mu2)^2/r1^5+3.0*mu2*(u[1]-mu1)^2/r2^5
	df3y = 3.0*mu1*(u[1]+mu2)*u[2]/r1^5+3.0*mu2*(u[1]-mu1)*u[2]/r2^5
	df3vx = 0
	df3vy = 2

	#derivatives f4
	df4x = 3.0*mu1*(u[1]+mu2)*u[2]/r1^5+3.0*mu2*(u[1]-mu1)*u[2]/r2^5
	df4y =  1.0-mu1/r1^3-mu2/r2^3+3.0*mu1*(u[2])^2/r1^5+3.0*mu2*(u[2])^2/r2^5
	df4vx = -2
	df4vy = 0

	du[5] = vxm
	du[6] = vym
	du[7] = df3x*xm + df3y*ym + df3vx*vxm + df3vy*vym
	du[8] = df4x*xm + df4y*ym + df4vx*vxm + df4vy*vym
	#megno evolve
	f = u[5]*du[5] + u[6]*du[6] + u[7]*du[7] + u[8]*du[8]
	d2 = u[5]^2 + u[6]^2 + u[7]^2 + u[8]^2

	# megno equations
	if t==0 # need check at t=0 to avoid overflows caused by 0 on the denominator
		chaosind1 = (f/d2) * (t + 1e-16)
		du[9] = chaosind1
		du[10] = 2*u[9]/(t + 1e-16)
	else
		chaosind1 = (f/d2) * t
		du[9] = chaosind1
		du[10] = 2*u[9]/t
	end

end

# solver
p = μ
prob = ODEProblem(cr3bp_rhs,u0,tspan,p)
@timeit to "sol" solution2 = solve(prob,Vern9(),reltol = 1e-16,abstol = 1e-16, maxiters = 1e8, saveat = t_end/numberofpoints)

df = DataFrame(solution2)
println("points:",length(df.timestamp))
println("time:",df.timestamp[end]/(2*pi))

"""
Checking if the cte error increases through the time
"""
jacobicte = []
for i in 1:length(df.timestamp)
	x= df.value1[i]
	y= df.value2[i]
	vx= df.value3[i]
	vy= df.value4[i]
	r1 = ((x + μ)^2 + y^2)^(1/2)
	r2 = ((-1 + x + μ)^2 + y^2)^(1/2)
	jacobi = (x^2 + y^2 - vx^2 - vy^2 + 2*((1-μ)/r1 + μ/r2))
	append!(jacobicte,jacobi)
end

p1 = scatter(df.timestamp,jacobicte, label="Jacobi Constant")
p2 = scatter(df.value1,df.value2)
print_timer(to::TimerOutput)
#p4 = plot(df.value9)
np= []
np2 = []

for i in 1:length(df.timestamp)
	b= df.value10[i]/df.timestamp[i]
	append!(np,b)
end


p3 = plot(df.timestamp,np, label=" MEGNO <Y>",  legend=:bottomright)
println("FINAL MEGNO: ", np[end])
plot(p1,p2,p3)
6

Is your f function non-allocating?

7

What you mean ? I don’t get it. Could you elaborate?

8

Ok my bad i got it now.

I’m not sure but i believe it is allocating i’ll try to not alocate it.