Hello,
I have set an ODEProblem object, but the procedure is stopped (although I still get t a solution) because a higher maxiters is needed.
How can I check what is the default value and what is the syntax to increase the value?
Thank you
https://diffeq.sciml.ai/stable/basics/common_solver_opts/#Miscellaneous
EDIT: In my modest experience, running into maxiters may be a sign that something is wrong with your model. If it is stopping at some discontinuity you may need to do something structural like using callbacks to address a change in the model behavior at that point.
Yes. Or you’re using a non-stiff ODE solver on a stiff problem. Usually if you hit maxiters you’re doing something wrong. Though there are cases where you just truly need more iterations.
That makes sense. I have the following:
function doubleInfect!(du, u, p, t)
μ, ν, κ, φ, ω, β, ρ, τ, η = p
#=
du[1] = susceptible
du[2] = infected
du[3] = resistant
du[4] = phages
=#
TOT = u[1]+u[2]+u[3]
du[1] = (μ * u[1]) * (1 - TOT/κ) - (φ * u[1] * u[3]) - (ω * u[1])
du[2] = (φ * u[1] * u[3]) - (η * u[2]) - (ω * u[2])
du[3] = ((ν * u[4]) * (1 - TOT/κ)) - (ω * u[4])
du[4] = (β * η * u[2]) - (ρ * φ * u[1] * u[3]) - (ω * u[3])
end
mu = 0.47 # maximum growth rate susceptible (B. longum)
nu = 0.72 # maximum growth rate resistant (E. coli)
kappa = 2.2*10^7 # maximum population density
phi = 10.0^-9 # adsorption rate
psi = 10.0^-9 # adsorption rate alternative
omega = 0.05 # outflow
eta = 1.0 # lyse rate
Eta = 1.0 # lyse rate alternative
beta = 50.0 # burst size
Beta = 50.0 # burst size alternative
rho = 0.6 # reinfection rate
tau = 3.62 # latency time
tmax = 4000.0 # time span 0-tmax
s0 = 50000.0 # initial susceptible population
i0 = 1.0e-9 # initial infected population
v0 = 80.0 # initial phage population
0 = 500.0 # initial resistant population
u0 = [s0, i0, r0, v0]
parms = [mu, nu, kappa, phi, omega, beta, rho, tau, eta]
tspan = (0.0, tmax)
prob = ODEProblem(doubleInfect!, u0, tspan, parms)
soln = solve(prob, AutoVern7(Rodas5()))
I changed the algorithm from Tsit5() to AutoVern7(Rodas5()) and AutoTsit5(Rosenbrock23()), but I always get:
julia> prob = ODEProblem(doubleInfect!, u0, tspan, parms)
ODEProblem with uType Array{Float64,1} and tType Float64. In-place: true
timespan: (0.0, 4000.0)
u0: [50000.0, 1.0e-9, 500.0, 80.0]
julia> soln = solve(prob, AutoVern7(Rodas5()))
┌ Warning: Interrupted. Larger maxiters is needed.
└ @ DiffEqBase ~/.julia/packages/DiffEqBase/3iigH/src/integrator_interface.jl:329
retcode: MaxIters
Interpolation: automatic order switching interpolation
What is the error here? How can I solve it? I get a solution, but I don’t like having errors dangling around…
Thank you
Are you sure you wrote down the equations you wanted? Your model doesn’t make too much sense.
du[3] = ((ν * u[4]) * (1 - TOT/κ)) - (ω * u[4])
simplifies with your values to du[3] = 0.68*u[4], so if the concentration of phages is always positive, then then the number of resistant diverges to infinity. As it diverges, TOT goes to infinity so (1 - TOT/κ) is going to go negative, so you’re going to then get very large negative terms. So your ODE won’t stay positive in u[1] (also the φ * u[1] * u[3] term). Once those two are negative, u[2] goes negative and…
I assume this isn’t what you wanted… but it’s what you told the computer to do. My guess is that one of those u[4] values is really u[3], so your equation should’ve been:
du[3] = ((ν * u[4]) * (1 - TOT/κ)) - (ω * u[3])
You are right, there we some problems with the indices. The model comes from the book Weitz’s Quantitative viral ecology, and the ODEs are:

which I converted in:
and then I added a bacterium that is not affected by phages:
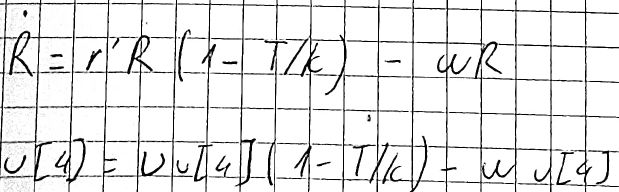
hence:
function doubleInfect!(du, u, p, t)
μ, ν, κ, φ, ω, β, τ, η = p
#=
du[1] = susceptible
du[2] = infected
du[3] = resistant
du[4] = phages
=#
TOT = u[1]+u[2]+u[4]
du[1] = (μ * u[1]) * (1 - TOT/κ) - (φ * u[1] * u[3]) - (ω * u[1])
du[2] = (φ * u[1] * u[3]) - (η * u[2]) - (ω * u[2])
du[3] = (β * η * u[2]) - (φ * u[1] * u[3]) - (ω * u[3])
du[4] = (ν * u[4]) * (1 - TOT/κ) - 0 - (ω * u[4])
end
# parameters
mu = 0.47 # maximum growth rate susceptible (B. longum)
nu = 0.72 # maximum growth rate resistant (E. coli)
kappa = 2.2*10^7 # maximum population density
phi = 10.0^-9 # adsorption rate
psi = 10.0^-9 # adsorption rate alternative
omega = 0.05 # outflow
eta = 1.0 # lyse rate
Eta = 1.0 # lyse rate alternative
beta = 50.0 # burst size
Beta = 50.0 # burst size alternative
rho = 0.6 # reinfection rate
tau = 3.62 # latency time
tmax = 4000.0 # time span 0-tmax
s0 = 50000.0 # initial susceptible population
i0 = 0.0 # initial infected population
v0 = 80.0 # initial phage population
r0 = 0.0 # initial resistant population
u0 = [s0, i0, r0, v0]
parms = [mu, nu, kappa, phi, omega, beta, tau, eta]
tspan = (0.0, tmax)
# delay infection
condition(u, t, integrator) = t==1000 # time of inoculum
affect!(integrator) = integrator.u[3] += 500 # amount of inoculum
cb = DiscreteCallback(condition,affect!)
# implement model
prob = ODEProblem(doubleInfect!, u0, tspan, parms)
soln = solve(prob, AutoVern7(Rodas5()), callback=cb, tstops=[1000])
This time:
julia> prob = ODEProblem(doubleInfect!, u0, tspan, parms)
ODEProblem with uType Array{Float64,1} and tType Float64. In-place: true
timespan: (0.0, 4000.0)
u0: [50000.0, 0.0, 0.0, 80.0]
julia> soln = solve(prob, AutoVern7(Rodas5()), callback=cb, tstops=[1000])
retcode: Success
Interpolation: automatic order switching interpolation
t: 105-element Array{Float64,1}:
So the problem was indeed in the equations. Thank you


