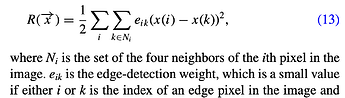Including Gradient Term in Optimization.jl

General Usage
1

Hi everyone :grinning:,

I’m trying to solve an optimization problem using Optimization.jl, but I’m struggling with incorporating a gradient term \nabla in the process. My cost function to minimize is:

\text{Cost} \left(T^{1}, T^{2}\right) = \|r^{A}\|^2 + \|r^{B}\|^2 + \|\nabla(T^{1})\|^2 + \|\nabla(T^{2})\|^2

where r^{A} and r^{B} involve log-sum-exponential terms:

r^{i}(T^{1}, T^{2}) = \log \left(\sum_K K \exp \left(-T^{1} v_K^{1} - T^{2} v_K^{2} \right) \right) - \log \left(Y^{i}\right)

Y^{i}, T^{1} and T^{2} are matrix of size n x m

I first tried without the gradient term \nabla to solve the problem “pixel by pixel” (basically with 2 nested for loop), and it works. I then tried to vectorize my residual function r over the whole matrix, but then the optimization is extremely slow and doesn’t work anymore.

function f(K, v₁, v₂, T₁, T₂) # the theoretical value, compared to $Y^{i}$ the measurments
    x = sum(K[i] * exp.(-v₁[k] * T₁ - v₂[k] * T₂) for k in axes(K)[1])
    return -log.(x / length(axes(K)[1]))
end

function r(T, p)
    K, v₁, v₂, matrix_A, matrix_B, s = p
    T₁, T₂ = view(T, :, 1:s), view(T, :, (s+1):size(T, 2)) # I concatenated T₁, T₂  to be able to use Optimization.jl
    sum((f(K.A, v₁, v₂, T₁, T₂) .- matrix_A).^2 .+
    (f(K.B, v₁, v₂, T₁, T₂) .- matrix_B).^2)
end

I think (?) vectorizing like that this is the only way to integrate the gradient term \nabla in the optimization, since the “pixel by pixel” approach does not give access to neighboring values in the matrix.
I don’t know if all this is clear ( I tried haha :slight_smile: ), but does anyone have experience with this kind of problem or any relevant example?

Thanks in advance!
fdekerm

2

Hi! Can you provide a complete example of your code (with all imports, function and variable definitions), and explain what you mean by “gradient” here?

1 Like
3

I can’t share the inputs for the functions, unfortunately.
For example in this article, they propose the following optimization problem:

Screenshot 2025-03-18 at 5.21.37 PM
Screenshot 2025-03-18 at 5.21.37 PM1062×154 11.3 KB

with
Screenshot 2025-03-18 at 5.21.02 PM
Screenshot 2025-03-18 at 5.21.02 PM1062×1106 123 KB

and the “gradient”

Screenshot 2025-03-18 at 5.25.06 PM
Screenshot 2025-03-18 at 5.25.06 PM1062×304 37.7 KB

They use images of N = 1024 * 768 = 786432 pixels, so the matrix A (size 2N *2N) is huge.
Likewise, the operation Screenshot 2025-03-18 at 5.29.52 PM is extremely heavy to realize on the whole matrix.

I’m not sure how to implement/vectorize the code to solve this type of problem with Optimiation.jl.
Thanks in advance for your help,
fdekerm

4

It’s a convex quadratic problem. Just take the derivative, set it equal to zero, and you have a system of linear equations that you can solve in a variety of ways, even for huge problems. In particular, it looks like the matrices here are all very sparse, so you can use sparse (or iterative) methods.

1 Like