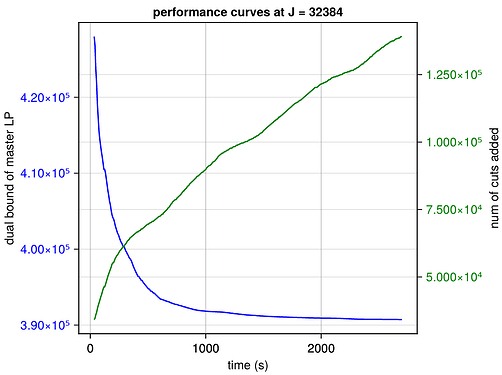
I’m happy to declare that I’ve devised a new architecture for the problem of this topic.
This algorithm is conceptually clearer and simpler than my previous ones. And it has better performance in practice. Here is my test:
After performing this algorithm, my memory occupation reaches 54.6GB.
code
import JuMP, Gurobi
import JuMP.value as ı
import Random # my std test case: seed = 44, K = 45, THREAD_FOR_BLOCKS = 253, so J = 11385
const my_seed = 44;
Random.seed!(my_seed);
const K = 128; # controls the problem scale
const GRB_ENV = Gurobi.Env();
const DEFAULT_THREADS = Threads.nthreads(); # Hardware Dependent
const THREAD_FOR_MAIN_LOOP = 1;
const THREAD_FOR_MASTER = 1;
const THREAD_FOR_BLOCKS = DEFAULT_THREADS - THREAD_FOR_MAIN_LOOP - THREAD_FOR_MASTER;
const J = (K)THREAD_FOR_BLOCKS; # Number of Blocks
begin # black box code used to create the physical model
function get_C_and_O()
C = [
# Case 1: Flat midday, strong evening peak
[10, 9, 9, 9, 10, 12, 15, 18, 20, 18, 16, 15, 14, 15, 16, 18, 22, 28, 32, 30, 26, 20, 15, 12],
# Case 2: Two peaks (morning + evening), midday dip
[12, 11, 11, 12, 14, 18, 24, 26, 22, 18, 15, 14, 13, 14, 18, 24, 30, 34, 32, 28, 22, 18, 15, 13],
# Case 3: Midday solar effect (cheapest at noon, peaks morning & evening)
[16, 15, 14, 14, 15, 18, 24, 30, 28, 22, 18, 12, 10, 12, 16, 22, 28, 34, 36, 32, 28, 24, 20, 18],
# Case 4: Steady climb during day, single high plateau evening
[8, 8, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 36, 34, 30, 26, 20, 14],
# Case 5: Inverted (very low off-peak overnight, high midday, gentle evening)
[5, 5, 5, 6, 8, 12, 18, 24, 28, 32, 36, 38, 36, 34, 30, 28, 26, 24, 22, 20, 18, 14, 10, 8]
]
O = [
# Case 1: Typical hot day (peak ~38°C around 15:00)
[28,28,27,27,28,29,31,33,35,36,37,38,38,38,37,36,35,34,32,31,30,29,29,28],
# Case 2: Extremely hot day (peak ~42°C, late afternoon peak)
[29,28,28,28,29,31,33,35,37,39,40,41,42,42,41,40,38,36,34,33,32,31,30,29],
# Case 3: Milder hot day (peak ~35°C, smooth curve)
[27,27,27,27,28,29,30,32,33,34,35,35,35,35,34,33,32,31,30,29,28,28,28,27],
# Case 4: Heatwave night (doesn’t cool much at night, peak 44°C)
[32,32,31,31,32,34,36,38,40,42,43,44,44,44,43,42,41,40,38,37,36,35,34,33],
# Case 5: Cool morning, sharp rise, peak ~39°C
[27,27,27,27,28,29,30,33,35,37,38,39,39,39,38,37,36,34,32,31,30,29,28,27]
]
return C[rand(1:5)], O[rand(1:5)]
end;
function get_pair_and_self_Rng(J)
d = J÷4
1:d, d+1:J # Rng1, Rng2
end;
function prev(t, d, T) return (n = t-d; n<1 ? T+n : n) end;
function pc_P_AC(O, OH, CND, Q_I, COP) return ceil(Int, ((maximum(O) - OH)CND + maximum(Q_I)) / COP) end;
function get_E_ES(Rng)::NamedTuple
M = rand(Rng) # Max E
i = rand(0:M) # initial SOC _is_ this value
e = rand(0:min(M, 21)) # ending SOC should ≥ this value
(; i, M, e)
end;
function add_ES_module!(model, P_ES, E_ES)
pES = ( # eES is dependent variable
c = JuMP.@variable(model, [1:T], lower_bound = 0),
d = JuMP.@variable(model, [1:T], lower_bound = 0)
); bES = JuMP.@variable(model, [1:T], Bin)
JuMP.@constraint(model, pES.c .≤ (bES)P_ES.c)
JuMP.@constraint(model, pES.d .≤ (1 .- bES)P_ES.d)
eES = JuMP.@variable(model, [t=1:T], lower_bound = t<T ? 0 : E_ES.e, upper_bound = E_ES.M)
JuMP.@constraint(model, [t=1:T], pES.c[t]*.95 - pES.d[t]/.95 == eES[t]-(t>1 ? eES[t-1] : E_ES.i))
return pES, bES, eES
end;
function gen_ac_data()::Tuple
CND = .5rand(1:7)
INR = rand(6:20)
COP = rand(2:.5:4)
Q_I = rand(3:9, T)
Q_BUS = rand(25:35)
OH = rand(24:29)
OΔ = rand(4:9)
P_AC = pc_P_AC(O, OH, CND, Q_I, COP)
return CND, INR, COP, Q_I, Q_BUS, OH, OΔ, P_AC
end;
function add_AC_module!(model, O, CND, INR, COP, Q_I, Q_BUS, OH, OΔ, P_AC)
pAC = JuMP.@variable(model, [1:T], lower_bound = 0, upper_bound = P_AC)
o = JuMP.@variable(model, [1:T], lower_bound = OH-OΔ, upper_bound = OH)
q = JuMP.@variable(model, [1:T], lower_bound = 0, upper_bound = Q_BUS)
JuMP.@constraint(model, [t=1:T], (O[t]-o[t])CND + Q_I[t] -q[t] -pAC[t]COP == (o[t<T ? t+1 : 1]-o[t])INR)
return o, q, pAC
end;
function add_U_module!(model, U)
bU::Matrix{JuMP.VariableRef} = JuMP.@variable(model, [t = 1:T, i = eachindex(U)], Bin)
JuMP.@constraint(model, sum(bU; dims = 1) .≥ true)
pU = JuMP.@expression(model, [t=1:T], sum(sum(bU[prev(t,φ-1,T), i]P for (φ,P) = enumerate(v)) for (i,v) = enumerate(U))) # Vector{JuMP.AffExpr}
return bU, pU
end;
function add_self_EV_module!(model, P_EV, E_EV) # self means a household in a block with cardinality 1
bEV, pEV = JuMP.@variable(model, [1:T], Bin), JuMP.@variable(model, [1:T])
JuMP.@constraint(model, (P_EV.m)bEV .≤ pEV)
JuMP.@constraint(model, pEV .≤ (P_EV.M)bEV)
JuMP.@constraint(model, sum(pEV) ≥ E_EV)
return bEV, pEV # bEV can be _inferred from_ pEV
end;
function pc_self_P_BUS(D, U, P_EV, E_EV, O, CND, INR, COP, Q_I, OH, OΔ, P_AC)::Int
model = get_simple_model()
bU, pU = add_U_module!(model, U)
bEV, pEV = add_self_EV_module!(model, P_EV, E_EV)
o, q, pAC = add_AC_module!(model, O, CND, INR, COP, Q_I, 0, OH, OΔ, P_AC) # Q_BUS = 0
pBus = JuMP.@variable(model)
JuMP.@constraint(model, pBus .≥ D + pU + pEV + pAC) # No G | ES
JuMP.@objective(model, Min, pBus)
@lock insset_lock push!(insset, model)
JuMP.optimize!(model)
@lock insset_lock delete!(insset, model)
ps, ts = JuMP.primal_status(model), JuMP.termination_status(model)
if ps != JuMP.FEASIBLE_POINT || ts ∉ [JuMP.OPTIMAL, JuMP.INTERRUPTED]
error(string(ps, ts))
end
val = JuMP.objective_value(model)
val > 0 || error("The self household has P_BUS = $val")
ceil(Int, val) # P_BUS
end;
function add_EV_1_module!(model, P_EV_1, E_EV_1)
bLent, pLent = JuMP.@variable(model, [1:T], Bin), JuMP.@variable(model, [1:T])
bEV_1, pEV_1 = JuMP.@variable(model, [1:T], Bin), JuMP.@variable(model, [1:T])
JuMP.@constraint(model, bEV_1 .≤ bLent)
JuMP.@constraint(model, (1 .- bLent)P_EV_1.m .≤ pLent)
JuMP.@constraint(model, pLent .≤ (1 .- bLent)P_EV_1.M)
JuMP.@constraint(model, (P_EV_1.m)bEV_1 .≤ pEV_1)
JuMP.@constraint(model, pEV_1 .≤ (P_EV_1.M)bEV_1)
JuMP.@constraint(model, sum(pEV_1) ≥ E_EV_1)
return bEV_1, pEV_1, bLent, pLent
end;
function add_EV_2_module!(model, P_EV_2, E_EV_2, bLent, pLent)
bEV_2, pEV_2 = JuMP.@variable(model, [1:T], Bin), JuMP.@variable(model, [1:T])
JuMP.@constraint(model, bEV_2 .≤ bLent)
JuMP.@constraint(model, (P_EV_2.m)bEV_2 .≤ pEV_2)
JuMP.@constraint(model, pEV_2 .≤ (P_EV_2.M)bEV_2)
JuMP.@constraint(model, sum(pEV_2 + pLent) ≥ E_EV_2)
return bEV_2, pEV_2
end;
function add_self_circuit_breaker_module!(model, P_BUS, D, pU, pEV, pAC)
pBus = JuMP.@variable(model, [1:T], lower_bound = 0, upper_bound = P_BUS)
JuMP.@constraint(model, pBus .≥ D + pU + pEV + pAC) # No G | ES
return pBus
end;
function add_circuit_breaker_pair_module!(model, P_BUS_1, P_BUS_2, p_ES, G, pLent, pEV_1, pU_1, pAC_1, D_1, pEV_2, pU_2, pAC_2, D_2)
pBus_1 = JuMP.@variable(model, [1:T], lower_bound = -P_BUS_1, upper_bound = P_BUS_1)
pBus_2 = JuMP.@variable(model, [1:T], lower_bound = 0, upper_bound = P_BUS_2)
JuMP.@constraint(model, pBus_1 .== p_ES.c -p_ES.d -G + pLent + pEV_1 + pU_1 + pAC_1 + D_1)
JuMP.@constraint(model, pBus_2 .≥ pEV_2 + pU_2 + pAC_2 + D_2)
return pBus_1, pBus_2
end;
function get_a_paired_block(O)::NamedTuple
model = get_simple_model() # for a block who has a lender and a borrower house
# 6 lines
G = rand(0:17, T)
D_1 = rand(0:5, T)
P_ES, E_ES = (c = rand(1:6), d = rand(1:6)), get_E_ES(19:55)
U_1 = [rand(1:4, rand(2:5)) for _ = 1:rand(1:4)] # each entry is a cycle vector of an uninterruptible load
P_EV_1, E_EV_1 = (m = rand((1., 1.5)), M = rand(3:7)), rand(10:39)
CND_1, INR_1, COP_1, Q_I_1, Q_BUS_1, OH_1, OΔ_1, P_AC_1 = gen_ac_data()
# lender house
pES, bES, eES = add_ES_module!(model, P_ES, E_ES)
bU_1, pU_1 = add_U_module!(model, U_1)
bEV_1, pEV_1, bLent, pLent = add_EV_1_module!(model, P_EV_1, E_EV_1)
o_1, q_1, pAC_1 = add_AC_module!(model, O, CND_1, INR_1, COP_1, Q_I_1, 0, OH_1, OΔ_1, P_AC_1) # Q_BUS = 0
# 4 lines
D_2 = rand(0:5, T) # borrower house
U_2 = [rand(1:4, rand(2:5)) for _ = 1:rand(1:4)] # each entry is a cycle vector of an uninterruptible load
P_EV_2, E_EV_2 = (m = rand((1., 1.5)), M = rand(3:7)), rand(10:39)
CND_2, INR_2, COP_2, Q_I_2, Q_BUS_2, OH_2, OΔ_2, P_AC_2 = gen_ac_data()
# borrower house
bU_2, pU_2 = add_U_module!(model, U_2)
bEV_2, pEV_2 = add_EV_2_module!(model, P_EV_2, E_EV_2, bLent, pLent)
o_2, q_2, pAC_2 = add_AC_module!(model, O, CND_2, INR_2, COP_2, Q_I_2, 0, OH_2, OΔ_2, P_AC_2) # Q_BUS = 0
# determine the circuit breaker limit
pBus_2 = JuMP.@variable(model, [1:T], lower_bound = 0)
temp_x = JuMP.@variable(model)
temp_c = JuMP.@constraint(model, pBus_2 .== temp_x)
JuMP.@constraint(model, pBus_2 .≥ pEV_2 + pU_2 + pAC_2 + D_2)
JuMP.@objective(model, Min, temp_x)
@lock insset_lock push!(insset, model)
JuMP.optimize!(model)
@lock insset_lock delete!(insset, model)
ps, ts = JuMP.primal_status(model), JuMP.termination_status(model)
if ps != JuMP.FEASIBLE_POINT || ts ∉ [JuMP.OPTIMAL, JuMP.INTERRUPTED]
error(string(ps, ts))
end
temp_float64 = ı(temp_x)
temp_float64 > 0 || error("common pBus_2 has value $temp_float64")
P_BUS_2 = ceil(Int, temp_float64)
JuMP.delete(model, temp_c)
JuMP.delete(model, temp_x)
JuMP.set_upper_bound.(pBus_2, P_BUS_2)
temp_x = JuMP.@variable(model) # reuse the local name
JuMP.@constraint(model, -temp_x .≤ pES.c -pES.d -G + pLent + pEV_1 + pU_1 + pAC_1 + D_1)
JuMP.@constraint(model, temp_x .≥ pES.c -pES.d -G + pLent + pEV_1 + pU_1 + pAC_1 + D_1)
JuMP.@objective(model, Min, temp_x)
@lock insset_lock push!(insset, model)
JuMP.optimize!(model)
@lock insset_lock delete!(insset, model)
ps, ts = JuMP.primal_status(model), JuMP.termination_status(model)
if ps != JuMP.FEASIBLE_POINT || ts ∉ [JuMP.OPTIMAL, JuMP.INTERRUPTED]
error(string(ps, ts))
end
temp_float64 = ı(temp_x)
temp_float64 > -1e-5 || error("pBus_1 has value $temp_float64")
P_BUS_1 = max(1, ceil(Int, temp_float64))
(;P_BUS_1, P_BUS_2, G, P_ES, E_ES, D_1, D_2, U_1, U_2, P_EV_1, P_EV_2,
E_EV_1, E_EV_2, CND_1, CND_2, INR_1, INR_2, COP_1, COP_2, Q_I_1, Q_I_2,
Q_BUS_1, Q_BUS_2, OH_1, OH_2, OΔ_1, OΔ_2, P_AC_1, P_AC_2)
end;
function get_a_self_block(O)::NamedTuple
D = rand(0:5, T) # base demand
U = [rand(1:4, rand(2:5)) for _ = 1:rand(1:4)] # each entry is a cycle vector of an uninterruptible load
P_EV, E_EV = (m = rand((1., 1.5)), M = rand(3:7)), rand(10:39)
CND, INR, COP, Q_I, Q_BUS, OH, OΔ, P_AC = gen_ac_data()
P_BUS = pc_self_P_BUS(D, U, P_EV, E_EV, O, CND, INR, COP, Q_I, OH, OΔ, P_AC)
(;P_BUS, D, U, P_EV, E_EV, CND, INR, COP, Q_I, Q_BUS, OH, OΔ, P_AC)
end;
function add_a_paired_block!(model, d::NamedTuple)::NamedTuple
# lender house
pES, bES, eES = add_ES_module!(model, d.P_ES, d.E_ES)
bU_1, pU_1 = add_U_module!(model, d.U_1)
bEV_1, pEV_1, bLent, pLent = add_EV_1_module!(model, d.P_EV_1, d.E_EV_1)
o_1, q_1, pAC_1 = add_AC_module!(model, O, d.CND_1, d.INR_1, d.COP_1, d.Q_I_1, 0, d.OH_1, d.OΔ_1, d.P_AC_1) # Q_BUS = 0
# borrower house
bU_2, pU_2 = add_U_module!(model, d.U_2)
bEV_2, pEV_2 = add_EV_2_module!(model, d.P_EV_2, d.E_EV_2, bLent, pLent)
o_2, q_2, pAC_2 = add_AC_module!(model, O, d.CND_2, d.INR_2, d.COP_2, d.Q_I_2, 0, d.OH_2, d.OΔ_2, d.P_AC_2) # Q_BUS = 0
# circuit breaker pair
pBus_1, pBus_2 = add_circuit_breaker_pair_module!(model, d.P_BUS_1, d.P_BUS_2,
pES, d.G, pLent, pEV_1, pU_1, pAC_1, d.D_1,
pEV_2, pU_2, pAC_2, d.D_2)
(;pBus_1, pBus_2, bLent, bES, bEV_1, bEV_2, bU_1, bU_2, q_1, q_2)
end;
function add_a_self_block!(model, d::NamedTuple)::NamedTuple
bU, pU = add_U_module!(model, d.U)
bEV, pEV = add_self_EV_module!(model, d.P_EV, d.E_EV)
o, q, pAC = add_AC_module!(model, O, d.CND, d.INR, d.COP, d.Q_I, 0, d.OH, d.OΔ, d.P_AC) # Q_BUS = 0
pBus = add_self_circuit_breaker_module!(model, d.P_BUS, d.D, pU, pEV, pAC)
(;pBus, bEV, bU, q)
end;
function fill_model_D_X!(v::Vector, X)
z = Threads.Atomic{Int}(J)
f = function(j)
p = j ∈ Rng1
X[j] = ifelse(p, add_a_paired_block!, add_a_self_block!)(
v[j],
ifelse(p, get_a_paired_block, get_a_self_block)(O)
)
Threads.atomic_sub!(z, 1)
print("\rrest = $(z.value), j = $j")
end
tasks, js_remains = map(j -> Threads.@spawn(f(j)), 1:J), Set(1:J)
t0 = time()
while !isempty(js_remains)
progress_j = 0
for j = js_remains
istaskdone(tasks[j]) && (progress_j = j; break)
end
if progress_j > 0
pop!(js_remains, progress_j)
t0 = time()
elseif time() - t0 > 15
foreach(Gurobi.GRBterminate ∘ JuMP.backend, insset)
printstyled("\nWarning: $(time()) terminate all solves\n"; color = :yellow)
@lock insset_lock empty!(insset)
t0 = time()
else
yield()
end
end
return foreach(wait, tasks)
end;
end;
function scalar!(X, j, m, x)
o = m.moi_backend
Gurobi.GRBgetdblattrelement(o, "X", Gurobi.c_column(o, JuMP.index(x[j])), view(X, j))
end;
value!(X, m, x) = foreach(j -> scalar!(X, j, m, x), eachindex(X));
function solve_mst_and_up_value!(m, s, θ, β)
JuMP.optimize!(m)
JuMP.termination_status(m) == JuMP.OPTIMAL || error() # The LP should always be solved to OPTIMAL
s.ub.x = JuMP.objective_bound(m)
value!(s.β, m, β)
value!(s.θ, m, θ)
end;
function shot!(ref; model = model, θ = θ, β = β, rEF = rEF)
s = rEF.x
@lock mst_lock solve_mst_and_up_value!(model, s, θ, β) # `s` gets updated/mutated here
s_tmp = ref.x
setfield!(ref, :x, s) # the ref gets updated here
setfield!(rEF, :x, s_tmp)
end;
function get_simple_model(; GRB_ENV = GRB_ENV)
m = JuMP.direct_model(Gurobi.Optimizer(GRB_ENV))
JuMP.set_silent(m)
JuMP.set_attribute(m, "Threads", 1)
m
end;
function initialize_out()
model = get_simple_model()
JuMP.@variable(model, β[1:T] ≥ 0)
JuMP.@constraint(model, sum(β) == 1) # ⚠️ special
JuMP.@variable(model, θ[1:J])
JuMP.@expression(model, out_obj_tbMax, sum(θ))
JuMP.@objective(model, Max, out_obj_tbMax)
# JuMP.@constraint(model, out_obj_tbMax ≤ an_UB)
return model, θ, β
end;
function bilin_expr(j, iˈı::Function, β; Rng1 = Rng1, model = model, X = X)
is_pair = j ∈ Rng1
JuMP.@expression(model, sum(iˈı(p)b for (b, p) = zip(β,
is_pair ? X[j].pBus_1 + X[j].pBus_2 : X[j].pBus
)))
end;
sublog(j) = println("block(j = $j)> no solution, go back to re-optimize...")
function subproblemˈs_duty(j; Ncuts = Ncuts, initialize = false, update_snap = false, ref = ref, inn = inn, model = model, θ = θ, β = β, COT = COT)
mj = inn[j]
while true
s = getfield(ref, :x)
JuMP.set_objective_function(mj, bilin_expr(j, identity, s.β))
JuMP.optimize!(mj)
ps, ts = JuMP.primal_status(mj), JuMP.termination_status(mj)
if ps !== JuMP.FEASIBLE_POINT || (ts !== JuMP.OPTIMAL && ts !== JuMP.TIME_LIMIT)
JuMP.set_attribute(mj, "Seed", rand(0:2000000000))
Threads.@spawn(:interactive, sublog(j))
continue
end
if !initialize
if update_snap
s = getfield(ref, :x)
end
s.θ[j] - bilin_expr(j, ı, s.β) > COT || return
end
con = JuMP.@build_constraint(θ[j] ≤ bilin_expr(j, ı, β))
@lock mst_lock JuMP.add_constraint(model, con)
Threads.atomic_add!(Ncuts, 1)
return
end
end;
const T = 24;
const (Rng1, Rng2) = get_pair_and_self_Rng(J);
const (C, O) = get_C_and_O(); # price and Celsius vector
const X = Vector{NamedTuple}(undef, J);
const COT = 0.5/J;
const an_UB = 30.0J
const mst_lock = ReentrantLock();
const is_inn_solving_vec = falses(J);
const inn = [get_simple_model() for j = 1:J];
const VCG = [NamedTuple[] for _ = 1:J]; # collect the Vertices found in the CG algorithm
const model, θ, β = initialize_out(); # ⚠️⚠️⚠️
const rEF = Ref((θ = fill(an_UB/J, J), β = fill(1/T, T), ub = Ref(an_UB)));
const ref = Ref((θ = fill(an_UB/J, J), β = fill(1/T, T), ub = Ref(an_UB))); # exposed solution
const insset = Set{JuMP.Model}()
const insset_lock = ReentrantLock();
const MAIN_TIME_LIMIT = 2700;
const LOG_TIME = 7;
const Ncuts = Threads.Atomic{Int}(0);
fill_model_D_X!(inn, X) # build the J blocks in parallel
foreach(mj -> JuMP.set_objective_sense(mj, JuMP.MIN_SENSE), inn)
foreach(mj -> JuMP.set_attribute(mj, "TimeLimit", 45), inn)
function warm() # to make the master problem have a _finite_ initial dual bound
tasks = map(j -> Threads.@spawn(subproblemˈs_duty(j; initialize = true)), 1:J)
foreach(wait, tasks)
end;
warm();
Ncuts.value === J || error(); # each block contributes 1 cut to make the master have a finite initial dual bound
shot!(ref);
next(j, J) = j === J ? 1 : j+1;
ntasksaway(tasks) = count(!istaskdone, tasks); # num of tasks away (i.e. not controllable)
function mainlog(tasks, ref, Ncuts, tabs0)
a = ntasksaway(tasks)
ub = ref.x.ub.x
n = Ncuts.value
t = round(Int, time() - tabs0)
println("main> N_BlockTasks_Away = $a, ub = $ub, Ncuts = $n, $t sec")
end;
function main(; J = J, ref = ref, model = model, MAIN_TIME_LIMIT = MAIN_TIME_LIMIT, LOG_TIME = LOG_TIME, Ncuts = Ncuts)
tabs0 = time(); tabs1 = tabs0 + MAIN_TIME_LIMIT # Time control region, do NOT move this line
#################################################
Ncuts0 = Ncuts.value
j = 1
mst_task = Threads.@spawn(shot!(ref))
tasks = map(_ -> Threads.@spawn(missing), 1:J)
#################################################
tlog0 = time() # Logging control region, do NOT move this line
while proceed_main.x && time() < tabs1 # Run with a time limit, or you manually interrupt
if time() - tlog0 > LOG_TIME
Threads.@spawn(:interactive, mainlog(tasks, ref, Ncuts, tabs0))
tlog0 = time()
end
if istaskdone(mst_task)
Ncuts_now = Ncuts.value
if Ncuts_now !== Ncuts0 # detect if new cuts have been added to the master
if ntasksaway(tasks) < THREAD_FOR_BLOCKS
mst_task = Threads.@spawn(shot!(ref)) # master's duty
Ncuts0 = Ncuts_now
end
end
end
while ntasksaway(tasks) < THREAD_FOR_BLOCKS # for block subproblems
if istaskdone(tasks[j])
tasks[j] = Threads.@spawn(subproblemˈs_duty($j; update_snap = true))
end
j = next(j, J) # go to ask the next block
end
GC.safepoint()
end
end;
const proceed_main = Ref(true);
main_task = Threads.@spawn(main());
# manual interrupt
map(f -> f(main_task), (istaskdone, istaskfailed))
setfield!(proceed_main, :x, false)
map(f -> f(main_task), (istaskdone, istaskfailed))
##########################################################
# [post convergent]: recover a valid lower bound
# ref.x.ub.x is an upper (dual) bound of the master LP, it is invalid _unless_ the Lagrangian convex optimization is solved to global optimality
# Nonetheless, we can derive a valid lower bound (to the original MIP), by calculating the _exact_ ObjVals of `inn` vector
##########################################################
function subproblemˈs_optimal_objval(j; ref = ref, inn = inn)
mj = inn[j]
JuMP.set_attribute(mj, "TimeLimit", 24*3600)
s = getfield(ref, :x)
JuMP.set_objective_function(mj, bilin_expr(j, identity, s.β))
JuMP.optimize!(mj)
ts = JuMP.termination_status(mj)
ts === JuMP.OPTIMAL || error("j = $j, terminate = $ts")
JuMP.objective_value(mj)
end;
function get_pvv() # primal value vector, which is the OBJVAL counterpart of the θ vector
pvv = Vector{Float64}(undef, J);
Threads.@threads for j = 1:J
print("\r primal_recover> j = $j / $J = J, MIP calculating via th = $(Threads.threadid())")
pvv[j] = subproblemˈs_optimal_objval(j)
end
pvv
end;
pvv = get_pvv();
ub = ref.x.ub.x # 390724.7612921933
lb = sum(pvv) # 390699.11541988095 ⚠️ The expression is problem-dependent, there is a common_part in general
agap = ub - lb # result agap of the convex CTPLN problem
rgap = agap / lb # 6.564097869738892e-5, i.e. less than 0.01%