How to utilize all cores when operating on large matrices

General Usage
1

I have a relatively large matrix (approximate size 50000x50000) that I need to bulk divide by numbers in a separate matrix of the same shape. The code does something simple like

V = A ./ B

It seems to utilize only a single core. Is there any way to make it use some number of cores to speed things up?

I tried setting JULIA_NUM_THREADS to 4 but it doesn’t seem to do anything.

2

I am not sure you will get any good speedup since an operation like this tends to be memory bounds.

You could perhaps play around with stuff like c++ - Element-wise vector-vector multiplication in BLAS? - Stack Overflow but that is only for multiplication, and from my testing, it seemed slower anyway.

3

IIUC (not an expert), this strongly depends on the architecture, and some machines have a memory bandwidth that scales with the number of cores.

edit: also the question is valid for more compute-bound kernels

4

See https://github.com/JuliaLang/julia/issues/19777 for threaded broadcast in particular.

5

Hi,

For strongly memory bound problems (like your previous post on array sum) and on a classical Desktop you may have some speed-up (x2-4) if you have several (2-4) memory channels. It is usually not the case on a laptop. Actually a floating point division takes some cycles and multithreading could be interesting.

In any case, I understood (from the previous link) that multithreading is not implicit for broadcast (which is a good think because it is difficult to anticipate if your code will be nested in another multithreaded context).

A possible solution if you have a strong interest in defining A and B separately, would be to fuse the div operation with the algorithm that uses V. A lazy definition of V could be nice :wink:

The curve corresponding to a MT+simd version your sum:

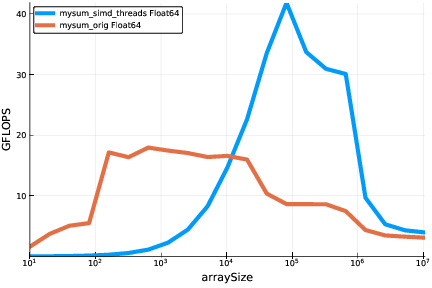
gflops_4t

And the corresponding snippet:

function mysum_simd_threads(a::Vector)
    total = zero(eltype(a))
    n=length(a)
    nchunk=4
    partialsum=zeros(eltype(a),nchunk)
    chunksize=n÷nchunk
    Threads.@threads for c=1:nchunk
        imin=(c-1)*chunksize+1
        imax=imin+chunksize-1
        stotal = zero(eltype(a))
        @simd for i=imin:imax
            @inbounds stotal += a[i]
        end
        partialsum[c]=stotal
    end
    total=sum(partialsum)
    for i=nchunk*chunksize+1:n
        total+=a[i]
    end
    return total
end
3 Likes