How to plot a impulse unit function using Plots.jl and SymPy.jl?

General Usage
,
1

Hello. Good evening.

I’m doing all exercises of the Sadiku’s book in julia programming.

The code is in github

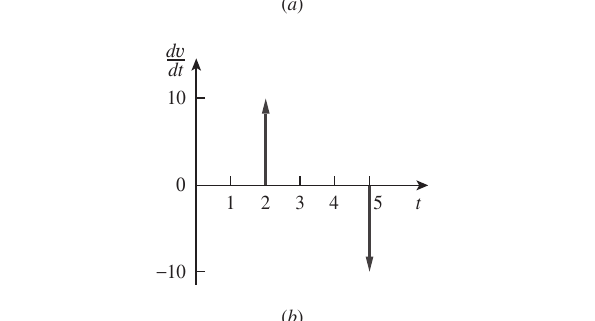
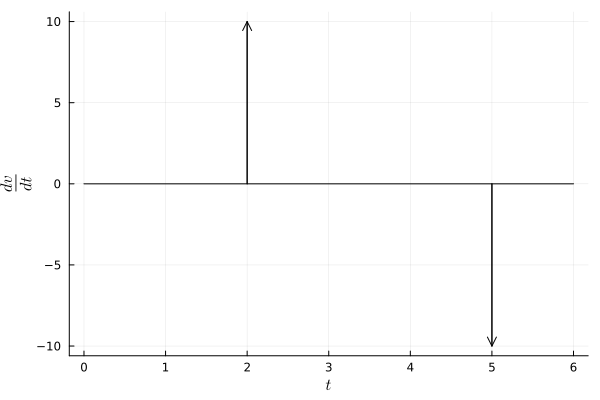
Im stucked to plot the impulse unit function after get it differentiating the unit step function.
The plot I get is only a line in zero, as plots.jl cant understand that the interval is all zero for values != t0. May someone help?

code:

let
	@syms t t₀

	u = sympy.Piecewise(
		(0, Lt(t, 0)),
		(1, Gt(t, 0))
	)
	@info u
	uₜ₀ = subs(u, t=> t - t₀)
	vₜ = 10(subs(uₜ₀, t₀=>2) - subs(uₜ₀, t₀=>5))
	@info vₜ
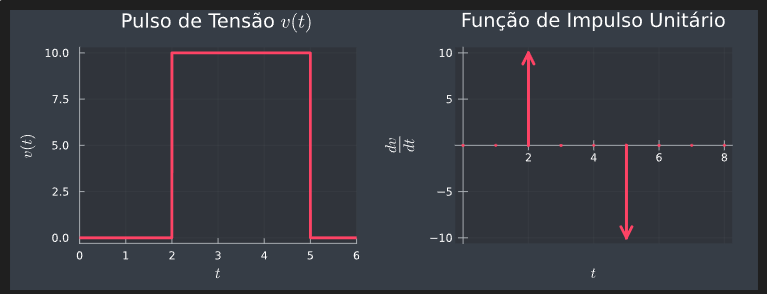
	p1 = plot(vₜ, xlims=(0, 6), lw=3, legend=:none, size=(400, 300))
	xlabel!(L"t")
	ylabel!(L"v(t)")
	title!(L"Pulso de Tensão $v(t)$")

	δ = diff(vₜ)
	# Ainda não sei como plotar a função de impulso unitário.
	@info δ
    plot( δ)
end

Results issues

image
image600×400 6.98 KB

Correct

image
image595×321 3.58 KB

2

Hi,

First of all, mathematically speaking a step function simply is not differentiable at the location of the step (according to the usual notion of differentiability), so in particular the derivative is not a dirac impulse. At every other point the derivative does exist and is zero.

I’m not very familiar with SymPy (and had to rely on PythonCall to get it working), but if I understand correctly, you’re explicitly not defining the function u: t \mapsto u(t) at t = 0. Consequently, δ will not be defined in 2 or 5. This is not related to the fact that the shifted u is non-differentiable here, just that you did not include it in the domain.

julia> δ
Python: 10*Piecewise((0, (t > 2) | (t < 2))) - 10*Piecewise((0, (t > 5) | (t < 5)))

julia> δ.subs(t, 2)
Python: nan

julia> δ.subs(t, 5)
Python: nan

If you would define u at t = 0 via Ge(t, 0), I get

julia> δ
Python: 0

so we still have issues with the non-differentiability.

In any case, if you want to recreate the plot, you could just manually add arrows

using Plots, LaTeXStrings

plot([0., 6.], [0., 0.], color=:black,
     xlabel=L"t", ylabel=L"$\frac{dv}{dt}$", legend=:none)
plot!([2., 2.], [0., 10.], arrow=true, color=:black, )
plot!([5., 5.], [0., -10.], arrow=true, color=:black)

arrows
arrows600×400 3.2 KB

(I’m not sure how to get the axes to intersect at the origin in Plots.jl.)

1 Like
3

Your derivative returns nan at both 2 and 5. This function gives it a value and then plots (the arrow works with GR at least)

## δ(2) is nan; so this adjusts
f(x) = isnan(δ(x)) ? float(vₜ(x+.001) - vₜ(x-.001)) : float(δ(x))
plot(0:8, f; linetype=:sticks, arrow=true, framestyle=:origin)

(Strangely, I thought defining u so it is defined at 0 might make this work, but that gives back a 0 derivative.)

1 Like
4

Hello friend. Thank you. Was a nice solution.

let
	@syms t t₀

	u = sympy.Piecewise(
		(0, Lt(t, 0)),
		(1, Gt(t, 0))
	)
	@info u
	uₜ₀ = subs(u, t=> t - t₀)
	vₜ = 10(subs(uₜ₀, t₀=>2) - subs(uₜ₀, t₀=>5))
	@info vₜ
	p1 = plot(vₜ, xlims=(0, 6), lw=3, legend=:none, size=(400, 300))
	xlabel!(L"t")
	ylabel!(L"v(t)")
	title!(L"Pulso de Tensão $v(t)$")

	δ = diff(vₜ)
	# Ainda não sei como plotar a função de impulso unitário.
	@info δ
	f(x) = isnan(δ(x)) ? float(vₜ(x+001) - vₜ(x-.001)) : float(δ(x))
	p2 = plot(0:8, f;
		 linetype=:sticks, arrow=true,
		 framestyle=:origin, legend=:none, lw=3,
		 xlabel=L"t", ylabel=L"\frac{dv}{dt}",
		 title="Função de Impulso Unitário"
		)
	plot(p1, p2, layout=(1, 2), size=(800, 300), margin=5Plots.mm)
	
end

image
image767×294 10.6 KB

5

Hello. Thank you to help. I pretty apreciate.
Yes, but this way Im cheating to get the graphs, and indeed, the exception in this impulse is nan, because <= or >= is not defined. I just got the derivative, but yes, a step function can be differentiated, and it gives me a impulse function. This exercise is meant to prove that.

6

You can try sympy.Heaviside(t) for your u. This will integrate as expected once differentiated.

For plotting you still would have to work to get the right plot as evaluating the derivative at 2 or 5 does not return a numeric value, rather this:

julia> let
       u = sympy.Heaviside(t)
       uₜ₀ = subs(u, t=> t - t₀)
       vₜ = 10(subs(uₜ₀, t₀=>2) - subs(uₜ₀, t₀=>5))
       δ = diff(vₜ)
       δ(2)
       end
10⋅δ(0)

Trying this function might be of interest, but you need to make sure 2 and 5 are points that are chosen to be plotted

f(x) = iszero(δ(x)) ? 0.0 : convert(Float64, (δ(x).o.args[1]))
2 Likes
7

Well, you have to cheat somewhere :slight_smile: , be it at the notion of derivative (ideally at the SymPy-level, cf. j_verzani’s second reply), the evaluation of some partially defined function (cf. j_verzani’s first reply; note that this is not a central finite difference approximation of the derivative, which would also divide by .002), or in the plots.

1 Like