Hello,
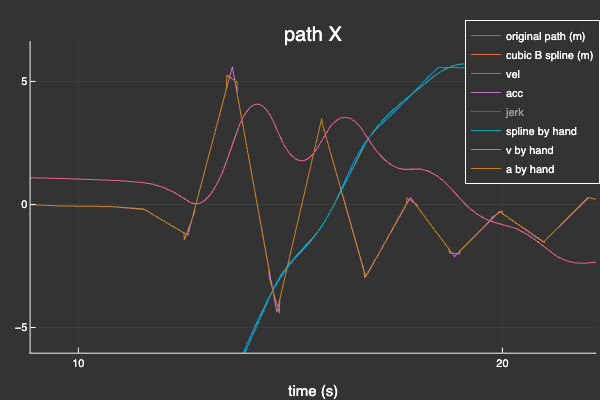
Given some data points tx, x. I would like to represent the path tx,x as well as its first and second derivative. I need my path to be C² continuous and small. It will be running in embedded C++
I have a set of data points which I curve fit with
Ax = BSplineApprox(x, tx, poly_deg, nb_pts_approx, :Uniform, :Uniform)
Then I didn’t find an easy way to obtain the knots and control points so I used forwardDiff to obtain the velocity.
velx(t) = ForwardDiff.derivative(x → Ax(x), t)
now assuming we remain at the knots
tc = collect(range(0,tx[end],nb_pts_approx))
PATH_X = Ax(tc)
PATH_VX = velx.(tc)
And now, I’m trying to use the Hermite cubic basis functions to reconstruct my segments (with appropriate scaling / change of variable), but the acceleration is discontinuous.
Am I confusing splines and cubis hermite polynomial?
How can I transport the spline data into my embedded system and reconstruct the path in real time?
I guess I could use a quintic spline and quintic hermite polynomial, but that would be an overkill…