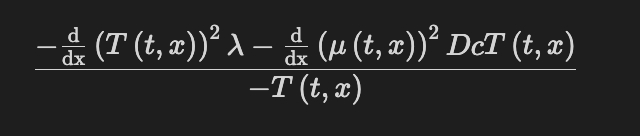Hi everyone,
I’m trying out a basic exercise which consists in generating the heat transfer equation (1D diffusion) by substitution the expressions of heat and heat flux in a balance equation, assuming constant coefficients.
using Symbolics
@variables t x
@variables U(t,x) qu(t,x) T(t,x)
@variables λ Cp
fu = Dt(U) == - dx(qu)
fu = substitute(fu, [qu=>-λ*dx(T), U=>Cp*T])
fu = simplify( expand_derivatives( fu ), expand=true)
It works and gives the output:

however it comes with an extra set of parenthesis and weirdly looking partial derivatives. So one question is: do I proceed correctly?
Also to define the initial balance equation, is it correct to set:
fu = Dt(U) == - dx(qu)
or
fu = Dt(U) ~ - dx(qu)
?
Thanks for your feedbacks!
Hi all,
In relation to the initial post, would someone know how to further simplify expression:
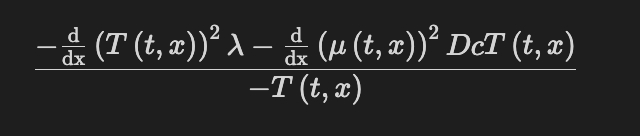
There is likely a way to cancel the minus sign and to simplify T/T in term on the right, but I haven’t managed so far.
Here’s the code:
using Symbolics, Latexify
@variables t x
@variables s(t,x) u(t,x) c(t,x) μ(t,x) ρ(t,x)
@variables qs(t,x) qu(t,x) qc(t,x)
@variables Qs
@variables T(t,x)
@variables λ Dc
Dt, dx = Differential(t), Differential(x)
solve = Symbolics.solve_for
subs = Symbolics.substitute;
# Define balances and axioms
fu = ρ*Dt(u) ~ - dx(qu)
fc = ρ*Dt(c) ~ - dx(qc)
fs = ρ*Dt(s) ~ - dx(qs) + Qs
LTE = Dt(u) ~ T*Dt(s) + μ*Dt(c)
latexify([fu; fc; fs; LTE])
# Evaluate entropy production
Qs1 = solve( fs, Qs )
Qs1 = subs(Qs1, Dt(s)=>solve(LTE,Dt(s)))
Qs1 = subs(Qs1, Dt(u)=>solve(fu,Dt(u)))
Qs1 = subs(Qs1, Dt(c)=>solve(fc,Dt(c)))
Qs1 = subs(Qs1, qu=>T*qs + μ*qc)
Qs1 = simplify_fractions(simplify(expand_derivatives(Qs1)))
TQs1 = T*simplify(subs(Qs1, [qs=>-λ/T*dx(T), qc=>-Dc*dx(μ)]), expand=true)
1 Like