[ANN] ModelingToolkitTolerances.jl

Specific Domains Modelling & Simulations
1

Very happy to announce a new package I’ve been working on to help debug ModelingToolkit.jl models. Using the power of Julia’s autodiff and the symbolics in ModelingToolkit.jl, it’s possible to estimate the error (or residual) of a model solution. Therefore it’s then possible to backout the optimal tolerance settings. Anyone who has struggled with DifferentialEquations.jl solver settings knows that sorting out a good solver choice with optimal abstol and reltol settings can be quite challenging.

For example, a gotcha that can occur is with a simple cooling model…

using ModelingToolkit
using ModelingToolkit: t_nounits as t, D_nounits as D
using OrdinaryDiffEq

T_inf=300; h=0.7; A=1; m=0.1; c_p=1.2
vars = @variables begin
    T(t)=301
end 
eqs = [
    D(T) ~ (h * A) / (m * c_p) * (T_inf - T)
]
@mtkbuild sys = ODESystem(eqs, t, vars, [])
prob = ODEProblem(sys, [], (0, 10))
sol = solve(prob, Tsit5())

The temperature is expect to drop smoothly from 301K to 300K, however the plot shows us a very strange result..

576×384 16.9 KB

What happened was simply the default tolerances don’t work well for this set of numbers. To fix the problem, we simply need to tighten the tolerance. But to what value? Should we change abstol or reltol? These values don’t have much physical meaning as it relates to the problem, therefore it’s a very difficult question to answer.

Now it’s possible to do the following…

using ModelingToolkitTolerances
resids = analysis(prob, Tsit5())
plot(resids)

576×384 21.5 KB

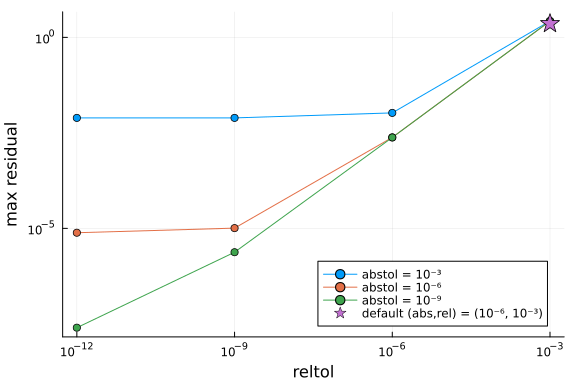
Now we can see that the default tolerance was giving a residual greater than 1. Also we can see that changing abstol does nothing in this case. Instead it’s necessary to drop reltol. Making the change gives the result we expect to see…

sol = solve(prob, Tsit5(); reltol=1e-6)
plot(sol; idxs=T)

576×384 10.1 KB

Have a look at the README for more examples and additional utilities. Let me know what you think. Contributions and suggestions for improvement are welcome!

10 Likes
2

Awesome work!

I’m interested in audio models that don’t ‘explode’ during realtime operation. Is it possible to generalise this search over all parameter ranges and all possible inputs?

3

That’s a good question. I think what you can do is use this package to check the residual for each case you run. For example, here I check the residual of the solution, update parameters, and check again. This kind of check could be put in a loop to reject bad result, or added into a loss function, etc…

using ModelingToolkit: t_nounits as t, D_nounits as D
using ModelingToolkitTolerances
using LinearAlgebra

pars = @parameters T_inf=300; h=0.7; A=1; m=0.1; c_p=1.2
vars = @variables begin
    T(t)=301
end 
eqs = [
    D(T) ~ (h * A) / (m * c_p) * (T_inf - T)
]
@mtkbuild sys = ODESystem(eqs, t, vars, pars)
prob = ODEProblem(sys, [], (0, 10))
sol = solve(prob, Tsit5())

# Check the residual
times = 0:0.1:10
res = residual(sol, times)
maximum(norm(res)) #2.5 <-- BAD

# Update parameters (same problem, in relative form)
prob′ = remake(prob; u0=[T=>1], p=[T_inf=>0])
sol′ = solve(prob′, Tsit5())

# Check the residual
res′ = residual(sol′, times)
maximum(norm(res′)) #7e-5 <-- OK!

Note: the residual object can contain multiple columns, therefore I use norm to merge them into 1 normalized vector and then take the maximum value.

1 Like